Matrix是threejs中一个比较重要的类，它主要用来处理三维空间中的变换。里面封装了很多工具函数，下面是一些重要函数的解析。Matrix官方文档地址 (opens new window)
# 1、decompose
这个函数 decompose 用于将一个 4x4 矩阵分解为平移（position）、旋转（quaternion）和缩放（scale）三个部分。
/**
* 将矩阵分解为位置、四元数和缩放因子
*
* @param {Vector3} position - 接收位置数据的Vector3对象
* @param {Quaternion} quaternion - 接收四元数数据的Quaternion对象
* @param {Vector3} scale - 接收缩放因子数据的Vector3对象
* @returns {Matrix4} 返回当前矩阵对象
*/
decompose( position, quaternion, scale ) {
const te = this.elements;
// 获取缩放因子
let sx = _v1.set( te[ 0 ], te[ 1 ], te[ 2 ] ).length();
const sy = _v1.set( te[ 4 ], te[ 5 ], te[ 6 ] ).length();
const sz = _v1.set( te[ 8 ], te[ 9 ], te[ 10 ] ).length();
// if determine is negative, we need to invert one scale
const det = this.determinant();
if ( det < 0 ) sx = - sx;
position.x = te[ 12 ];
position.y = te[ 13 ];
position.z = te[ 14 ];
// scale the rotation part
_m1.copy( this );
const invSX = 1 / sx;
const invSY = 1 / sy;
const invSZ = 1 / sz;
_m1.elements[ 0 ] *= invSX;
_m1.elements[ 1 ] *= invSX;
_m1.elements[ 2 ] *= invSX;
_m1.elements[ 4 ] *= invSY;
_m1.elements[ 5 ] *= invSY;
_m1.elements[ 6 ] *= invSY;
_m1.elements[ 8 ] *= invSZ;
_m1.elements[ 9 ] *= invSZ;
_m1.elements[ 10 ] *= invSZ;
quaternion.setFromRotationMatrix( _m1 );
scale.x = sx;
scale.y = sy;
scale.z = sz;
return this;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
以下是函数的逐步解析：
# 1.提取矩阵元素
const te = this.elements;
1
# 2.获取缩放因子
通过计算矩阵的各个列向量的长度，得到缩放因子
let sx = _v1.set( te[ 0 ], te[ 1 ], te[ 2 ] ).length();
const sy = _v1.set( te[ 4 ], te[ 5 ], te[ 6 ] ).length();
const sz = _v1.set( te[ 8 ], te[ 9 ], te[ 10 ] ).length();
1
2
3
2
3
# 3.检查行列式的符号
如果矩阵的行列式是负的，表示这个矩阵包含了一个反射操作。为了保持矩阵的几何意义，需要反转一个缩放因子。
const det = this.determinant();
if ( det < 0 ) sx = - sx;
1
2
2
# 4.提取平移部分
position.x = te[ 12 ];
position.y = te[ 13 ];
position.z = te[ 14 ];
1
2
3
2
3
# 5.提取旋转部分
复制矩阵，然后用缩放因子的倒数来缩放旋转部分，以分离出旋转矩阵
_m1.copy( this );
const invSX = 1 / sx;
const invSY = 1 / sy;
const invSZ = 1 / sz;
_m1.elements[ 0 ] *= invSX;
_m1.elements[ 1 ] *= invSX;
_m1.elements[ 2 ] *= invSX;
_m1.elements[ 4 ] *= invSY;
_m1.elements[ 5 ] *= invSY;
_m1.elements[ 6 ] *= invSY;
_m1.elements[ 8 ] *= invSZ;
_m1.elements[ 9 ] *= invSZ;
_m1.elements[ 10 ] *= invSZ;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 6.提取旋转四元数
将缩放后的矩阵传递给四元数对象，从而提取旋转信息。setFromRotationMatrix方法会在Quaternion类中进行详解
quaternion.setFromRotationMatrix( _m1 );
1
# 7.将缩放因子设置到 scale 对象中
scale.x = sx;
scale.y = sy;
scale.z = sz;
1
2
3
2
3
# 8.返回当前矩阵
return this;
1
# 2、determinant
这个 determinant 函数用于计算 4x4 矩阵的行列式。行列式是一个标量值，用于描述矩阵的某些属性，如是否可逆和变换的缩放因子。具体来说，行列式为 0 表示矩阵不可逆，行列式的符号表示变换的方向性（例如，是否包含反射操作）。
计算 4x4 矩阵的行列式的具体方法基于矩阵的分块展开法（Laplacian expansion）。这是一个递归的方法，通过计算子矩阵的行列式来求得原始矩阵的行列式。
determinant() {
const te = this.elements;
const n11 = te[ 0 ], n12 = te[ 4 ], n13 = te[ 8 ], n14 = te[ 12 ];
const n21 = te[ 1 ], n22 = te[ 5 ], n23 = te[ 9 ], n24 = te[ 13 ];
const n31 = te[ 2 ], n32 = te[ 6 ], n33 = te[ 10 ], n34 = te[ 14 ];
const n41 = te[ 3 ], n42 = te[ 7 ], n43 = te[ 11 ], n44 = te[ 15 ];
//TODO: make this more efficient
//( based on http://www.euclideanspace.com/maths/algebra/matrix/functions/inverse/fourD/index.htm )
return (
n41 * (
+ n14 * n23 * n32
- n13 * n24 * n32
- n14 * n22 * n33
+ n12 * n24 * n33
+ n13 * n22 * n34
- n12 * n23 * n34
) +
n42 * (
+ n11 * n23 * n34
- n11 * n24 * n33
+ n14 * n21 * n33
- n13 * n21 * n34
+ n13 * n24 * n31
- n14 * n23 * n31
) +
n43 * (
+ n11 * n24 * n32
- n11 * n22 * n34
- n14 * n21 * n32
+ n12 * n21 * n34
+ n14 * n22 * n31
- n12 * n24 * n31
) +
n44 * (
- n13 * n22 * n31
- n11 * n23 * n32
+ n11 * n22 * n33
+ n13 * n21 * n32
- n12 * n21 * n33
+ n12 * n23 * n31
)
);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
下面是这个函数的详细解析：
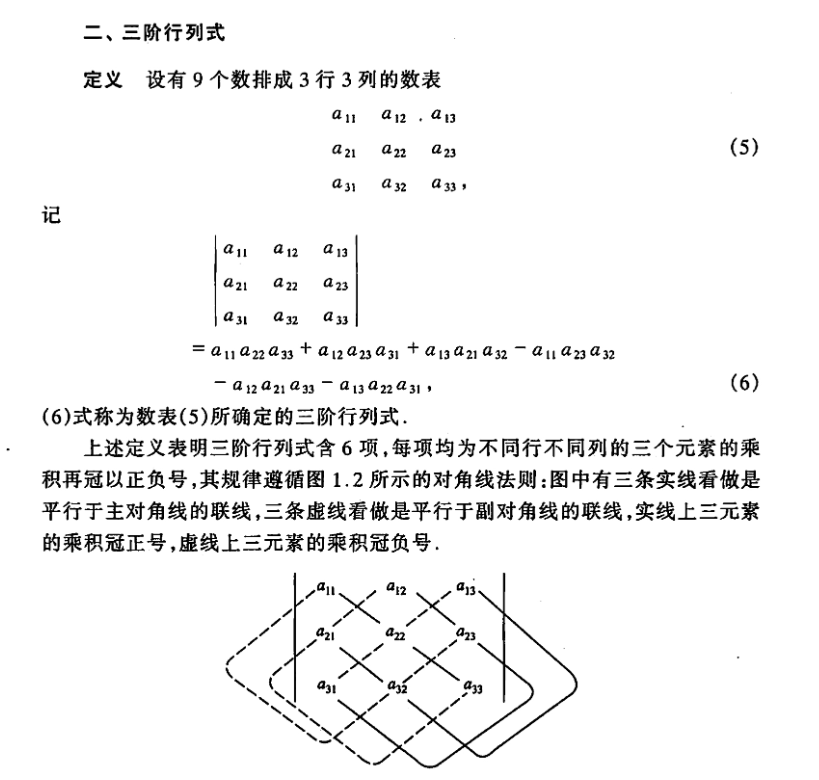
下面是三阶行列式的计算公式
# 1.提取矩阵元素
const te = this.elements;
const n11 = te[ 0 ], n12 = te[ 4 ], n13 = te[ 8 ], n14 = te[ 12 ];
const n21 = te[ 1 ], n22 = te[ 5 ], n23 = te[ 9 ], n24 = te[ 13 ];
const n31 = te[ 2 ], n32 = te[ 6 ], n33 = te[ 10 ], n34 = te[ 14 ];
const n41 = te[ 3 ], n42 = te[ 7 ], n43 = te[ 11 ], n44 = te[ 15 ];
1
2
3
4
5
6
7
2
3
4
5
6
7
# 2.行列式的计算公式
return (
n41 * (
+ n14 * n23 * n32
- n13 * n24 * n32
- n14 * n22 * n33
+ n12 * n24 * n33
+ n13 * n22 * n34
- n12 * n23 * n34
) +
n42 * (
+ n11 * n23 * n34
- n11 * n24 * n33
+ n14 * n21 * n33
- n13 * n21 * n34
+ n13 * n24 * n31
- n14 * n23 * n31
) +
n43 * (
+ n11 * n24 * n32
- n11 * n22 * n34
- n14 * n21 * n32
+ n12 * n21 * n34
+ n14 * n22 * n31
- n12 * n24 * n31
) +
n44 * (
- n13 * n22 * n31
- n11 * n23 * n32
+ n11 * n22 * n33
+ n13 * n21 * n32
- n12 * n21 * n33
+ n12 * n23 * n31
)
);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 3.分块展开法
也称为拉普拉斯展开，公式通过对矩阵的第4行进行展开（Laplacian expansion）,并计算每个子矩阵的3x3行列式。每个子矩阵由删除当前元素所在的行和列后形成。例如，对于 n41 元素，其余子矩阵（余子式）的行列式计算如下：
n41 * (
+ n14 * n23 * n32
- n13 * n24 * n32
- n14 * n22 * n33
+ n12 * n24 * n33
+ n13 * n22 * n34
- n12 * n23 * n34
)
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
# 4.符号交替
Laplacian expansion的每项前面都有一个符号，符号交替来自公式本身
n41 * (...) +
n42 * (...) +
n43 * (...) +
n44 * (...)
1
2
3
4
5
2
3
4
5
# 3、compose
将位置、四元数和缩放值组合成一个变换矩阵
/**
* 将位置、四元数和缩放值组合成一个变换矩阵
*
* @param position 位置向量
* @param quaternion 四元数
* @param scale 缩放向量
* @returns 返回当前对象
*/
compose( position, quaternion, scale ) {
const te = this.elements;
const x = quaternion._x, y = quaternion._y, z = quaternion._z, w = quaternion._w;
const x2 = x + x, y2 = y + y, z2 = z + z;
const xx = x * x2, xy = x * y2, xz = x * z2;
const yy = y * y2, yz = y * z2, zz = z * z2;
const wx = w * x2, wy = w * y2, wz = w * z2;
const sx = scale.x, sy = scale.y, sz = scale.z;
te[ 0 ] = ( 1 - ( yy + zz ) ) * sx;
te[ 1 ] = ( xy + wz ) * sx;
te[ 2 ] = ( xz - wy ) * sx;
te[ 3 ] = 0;
te[ 4 ] = ( xy - wz ) * sy;
te[ 5 ] = ( 1 - ( xx + zz ) ) * sy;
te[ 6 ] = ( yz + wx ) * sy;
te[ 7 ] = 0;
te[ 8 ] = ( xz + wy ) * sz;
te[ 9 ] = ( yz - wx ) * sz;
te[ 10 ] = ( 1 - ( xx + yy ) ) * sz;
te[ 11 ] = 0;
te[ 12 ] = position.x;
te[ 13 ] = position.y;
te[ 14 ] = position.z;
te[ 15 ] = 1;
return this;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# 4、makeRotationFromQuaternion
makeRotationFromQuaternion( q ) {
return this.compose( _zero, q, _one );
}
1
2
3
2
3
# 5、makeRotationFromEuler
/**
* 从欧拉角生成旋转矩阵
*
* @param euler 包含欧拉角的对象，包含x、y、z三个属性，表示绕X、Y、Z轴的旋转角度（以弧度为单位）
* @param euler.x 绕X轴的旋转角度（以弧度为单位）
* @param euler.y 绕Y轴的旋转角度（以弧度为单位）
* @param euler.z 绕Z轴的旋转角度（以弧度为单位）
* @param euler.order 欧拉角的旋转顺序，可选值有'XYZ'、'YXZ'、'ZXY'、'ZYX'、'YZX'、'XZY'
* @returns 当前的对象（包含旋转后的元素）
*/
makeRotationFromEuler( euler ) {
const te = this.elements;
const x = euler.x, y = euler.y, z = euler.z;
const a = Math.cos( x ), b = Math.sin( x );
const c = Math.cos( y ), d = Math.sin( y );
const e = Math.cos( z ), f = Math.sin( z );
if ( euler.order === 'XYZ' ) {
const ae = a * e, af = a * f, be = b * e, bf = b * f;
te[ 0 ] = c * e;
te[ 4 ] = - c * f;
te[ 8 ] = d;
te[ 1 ] = af + be * d;
te[ 5 ] = ae - bf * d;
te[ 9 ] = - b * c;
te[ 2 ] = bf - ae * d;
te[ 6 ] = be + af * d;
te[ 10 ] = a * c;
} else if ( euler.order === 'YXZ' ) {
const ce = c * e, cf = c * f, de = d * e, df = d * f;
te[ 0 ] = ce + df * b;
te[ 4 ] = de * b - cf;
te[ 8 ] = a * d;
te[ 1 ] = a * f;
te[ 5 ] = a * e;
te[ 9 ] = - b;
te[ 2 ] = cf * b - de;
te[ 6 ] = df + ce * b;
te[ 10 ] = a * c;
} else if ( euler.order === 'ZXY' ) {
const ce = c * e, cf = c * f, de = d * e, df = d * f;
te[ 0 ] = ce - df * b;
te[ 4 ] = - a * f;
te[ 8 ] = de + cf * b;
te[ 1 ] = cf + de * b;
te[ 5 ] = a * e;
te[ 9 ] = df - ce * b;
te[ 2 ] = - a * d;
te[ 6 ] = b;
te[ 10 ] = a * c;
} else if ( euler.order === 'ZYX' ) {
const ae = a * e, af = a * f, be = b * e, bf = b * f;
te[ 0 ] = c * e;
te[ 4 ] = be * d - af;
te[ 8 ] = ae * d + bf;
te[ 1 ] = c * f;
te[ 5 ] = bf * d + ae;
te[ 9 ] = af * d - be;
te[ 2 ] = - d;
te[ 6 ] = b * c;
te[ 10 ] = a * c;
} else if ( euler.order === 'YZX' ) {
const ac = a * c, ad = a * d, bc = b * c, bd = b * d;
te[ 0 ] = c * e;
te[ 4 ] = bd - ac * f;
te[ 8 ] = bc * f + ad;
te[ 1 ] = f;
te[ 5 ] = a * e;
te[ 9 ] = - b * e;
te[ 2 ] = - d * e;
te[ 6 ] = ad * f + bc;
te[ 10 ] = ac - bd * f;
} else if ( euler.order === 'XZY' ) {
const ac = a * c, ad = a * d, bc = b * c, bd = b * d;
te[ 0 ] = c * e;
te[ 4 ] = - f;
te[ 8 ] = d * e;
te[ 1 ] = ac * f + bd;
te[ 5 ] = a * e;
te[ 9 ] = ad * f - bc;
te[ 2 ] = bc * f - ad;
te[ 6 ] = b * e;
te[ 10 ] = bd * f + ac;
}
// bottom row
te[ 3 ] = 0;
te[ 7 ] = 0;
te[ 11 ] = 0;
// last column
te[ 12 ] = 0;
te[ 13 ] = 0;
te[ 14 ] = 0;
te[ 15 ] = 1;
return this;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
阅读量：