# 1、树的层序遍历从上到下打印二叉树 II (opens new window)
从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。 **解题思路:**利用栈来存储结点。每次遍历时,将当前结点的左右结点入栈,循环时依次出栈。
/**
* @param {TreeNode} root
* @return {number[]}
*/
//层序遍历 利用栈来存储节点
function levelOrder(root){
if(!node) return [];
const res=[],nodeQueue=[root];
let curNode=null;
while(nodeQueue.length){
curNode=nodeQueue.pop();
res.push(curNode.val);
curNode.left&&nodeQueue.push(curNode.left);
curNode.right&&nodeQUeue.push(curNode.right)
}
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 2、树的层序遍历2——II. 从上到下打印二叉树 II (opens new window)
从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。
/**
* @param {TreeNode} root
* @return {number[][]}
*/
//层序遍历
function levelOrder(root){
if(!root) return [];
const res=[],nodeQueue=[root];
let level=0,curNode=null,levelNodeNum;
//表示有多少层
while(nodeQueue.length){
res[level]=[];
levelNodeNum=nodeQueue.length;//第level层的节点个数
while(levelNodeNum--){
curNode=nodeQueue.pop();
res[level].push(curNode.val);
curNode.left&&nodeQueue.unshift(curNode.left);
curNode.right&&nodeQueue.unshift(curNode.right);
}
level++;
}
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 3、前序遍历二叉树的深度 (opens new window)
输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度为树的深度。 解题思路: 递归比较左右支树的深度,每次递归时深度加1.
/**
* @param {TreeNode} root
* @return {number}
*/
var maxDepth = function(root) {
if(!root) return 0;
//获当前左右子树的深度的较大值 并且+1
return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
};
2
3
4
5
6
7
8
9
# 4、前序遍历 二叉树的镜像 (opens new window)
请完成一个函数,输入一个二叉树,该函数输出它的镜像。 解题思路: 递归遍历整棵树,在递归时交换左右结点的位置。本质上是前序遍历。
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
function mirrorTree(root){
function levelOrder(node){
if(!node) return;
//前序遍历 跟左右
//交换左右节点的位置
const tempNode=node.left;
node.left=node.right;
node.right=tempNode;
//递归左右节点
levelOrder(node.left);
levelOrder(node.right);
}
levelOrder(root);
return root;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 5、前序遍历求根到叶子节点数字之和 (opens new window)
给定一个二叉树,它的每个结点都存放一个 0-9 的数字,每条从根到叶子节点的路径都代表一个数字。 例如,从根到叶子节点路径 1->2->3 代表数字 123。 计算从根到叶子节点生成的所有数字之和。 说明: 叶子节点是指没有子节点的节点。
/*
* @param {TreeNode} root
* @return {number}
*/
function sumNumbers(root){
const dfs=(node,sum)=>{
//表示该叶子节点不存在,则返回0
if(!node) return 0;
//树深度每加深一层,sum乘以10再加上当前节点的值
sum=sum*10+node.val;
if(!node.left&&!node.right){
//没有叶子节点了
return sum;
}else{
return dfs(node.left,sum)+dfs(node.right,sum)
}
}
return dfs(root,0);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 6、前序遍历对称的二叉树 (opens new window)
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/
2 2
/ \ /
3 4 4 3
function symmetricTree(root){
return root===null?true:dfs(root.left,root.right);
function dfs(l,r){
//没有左右节点的情况
if(l===null&&r===null) return true
/*
* 情况1 l=null,r!=null
* 情况2 l!=null,r===null
* 情况3 l!=null,r!=null l.val!=r.val
*/
if(l===null||r===null||l.val!==r.val) return false;
//递归左右子节点
return dfs(l.left,r.right)&&dfs(l.right,r.left);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 7、前序遍历平衡二叉树 (opens new window)
输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
3
/
9 20
/
15 7
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
1
/ \
2 2
/ \
3 3
/
4 4
返回 false 。
function isBalanced(root){
return recur(root)!==-1;
//深度递归
function recur(root){
if(!root) return 0;
//左子树的深度
const left=recur(root.left);
if(left===-1) return -1;
//右子树的深度
const right=recur(root.right);
if(right===-1) return -1;
//当节点root 左 / 右子树的深度差 \leq 1≤1 :则返回当前子树的深度,
return Math.abs(left-right)<2?Math.max(left,right)+1:-1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 8、二叉搜索树的最近公共祖先 (opens new window)
二叉搜索树具有以下性质:若它的左子树不为空,则左树上所有结点的值均小于它的根节点的值;若它右子树不为空,则右子树上所有结点的值均大于它的根节点的值;它的左、右子树也分别为二叉搜索树。 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 输出: 6 解释: 节点 2 和节点 8 的最近公共祖先是 6。 示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 输出: 2 解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
function lowestCommonAncestor(root, p,q) {
if(!root) return root;
if(p===q) return new TreeNode(p);
//根据题目条件 要么p,q在同侧,要么再异侧。在同侧则则p或q的值对应的结点是祖先结点,在异侧则根节点是它们的最近公共祖先。
while(root){
//根值大于给定值,则它的根植只可能在右边
if (root.val < q && root.val < p) {
root = root.right
}
//根值大于给定值,则它的根植只可能在左边
if (root.val > q && root.val > p) {
root = root.left
}
else { //p,q在异侧
return root
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 9、路径总和 (opens new window)
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/
4 8
/ /
11 13 4
/ \
7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
//方法 1 广度优先遍历
function hasPathSum(root,sum){
if(!root) return false;
const queueNode=[root];//存结点
const queueVal=[root.val];//存结点和
let tempNode,tempVal;
while(queueVal.length){
tempNode=queueNode.shift();//当前结点
tempVal=queueVal.shift();//当前结点对应的根节点到当前结点的路径和
if(!tempNode.left&&!tempNode.right){
if(tempVal===sum) return true;
}
if(tempNode.left){
queueNode.push(tempNode.left);
queueVal.push(tempVal+tempNode.left.val);
}
if(tempNode.right){
queueNode.push(tempNode.right);
queueVal.push(tempVal+ tempNode.right.val);
}
}
return false;
}
//方法 2 深度优先遍历
function hasPathSum(root,sum){
//表示该结点是空节点 此时sum的值肯定不等于它父节点的值,所以返回false
if(!root) return false;
//表示当前结点是叶子结点
if(!root.left&&!root.right){
return root.val===sum;
}
//先深度递归左子树
return hasPathSum(root.left,sum-root.val)||hasPathSum(root.right,sum-root.val);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 10、二叉搜索树的最近公共祖先 (opens new window)
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:"对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。"
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
2
3
4
5
6
7
8
/**
* @param {TreeNode} root
* @param {TreeNode} p
* @param {TreeNode} q
* @return {TreeNode}
*/
//迭代法
function lowestCommonAncestor(root, p, q) {
let node=root;
while(true){
if(node.val>p.val&&node.val>q.val){
node=node.left;
}else if(p.val>node.val&&q.val>node.val){
node=node.right;
}else{
break;
}
}
return node;
};
// 递归
function lowestCommonAncestor(root, p, q) {
const val=root.val;
if((p.val-val)*(q.val-val)<=0) return root;
if(p.val<val){
return lowestCommonAncestor(root.left,p,q);
}else{
return lowestCommonAncestor(root.right,p,q);
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 11、中序遍历 二叉搜索树的最小绝对差 (opens new window)
给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。
var getMinimumDifference = function(root) {
//因为是二叉搜索树,所以任意两节点的差的最小值。肯定是两个相邻节点差的最小值。
//中序遍历来遍历二叉搜索树,前一个值总是大于后面一个值
let prevValue=-1,res=Math.pow(2,31)-1;
const recursive=(node)=>{
if(!node) return;
//中序遍历 左根右
recursive(node.left);
if(prevValue!==-1){
//比较当前值与前一个值根的差与上一个最小差的大小
res=Math.min(res,node.val-prevValue);
}
prevValue=node.val;
recursive(node.right);
}
recursive(root);
return res;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 12、前序遍历左叶子之和 (opens new window)
/**
* @param {TreeNode} root
* @return {number}
*/
var sumOfLeftLeaves = function(root) {
let res=0;
/**
* @param {TreeNode} node
* @return {boolean} flag 用于标识是否是左子节点
*/
const recursive=(node,flag)=>{
if(!node) return;
//前序遍历
//判断是否是左子节点
if(flag&&!node.left&&!node.right) res+=node.val;
recursive(node.left,true);
recursive(node.right);
}
recursive(root);
return res;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 13、前序遍历单值二叉树 (opens new window)
如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时,才返回 true;否则返回 false。
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isUnivalTree = function(root) {
let prevValue=-1;
const recursive=node=>{
if(!node) return true;
if(prevValue!==-1){
//判断当前节点的值根上一个节点的值是否相等
if(prevValue!==node.val) return false;
}
prevValue=node.val;
//前序遍历(根左右) 先遍历左子树,后遍历右子树
return recursive(node.left)&& recursive(node.right);
}
return recursive(root);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 14、层序遍历(广度优先遍历) 二叉树的层平均值 (opens new window)
/**
* @param {TreeNode} root
* @return {number[]}
*/
var averageOfLevels = function(root) {
if(!root) return []
const res=[];
let queueNode=[root];
let sum,levelNum;
while(queueNode.length){
levelNum=queueNode.length;
sum=0;
res.push(levelNum);
while(levelNum--){
const tempNode=queueNode.shift();
sum+=tempNode.val;
tempNode.left&&queueNode.push(tempNode.left);
tempNode.right&&queueNode.push(tempNode.right);
}
res.push(sum/res.pop());
}
return res;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 15、层序遍历(广度优先遍历)N叉树的最大深度 (opens new window)
给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
例如,给定一个 3叉树 :
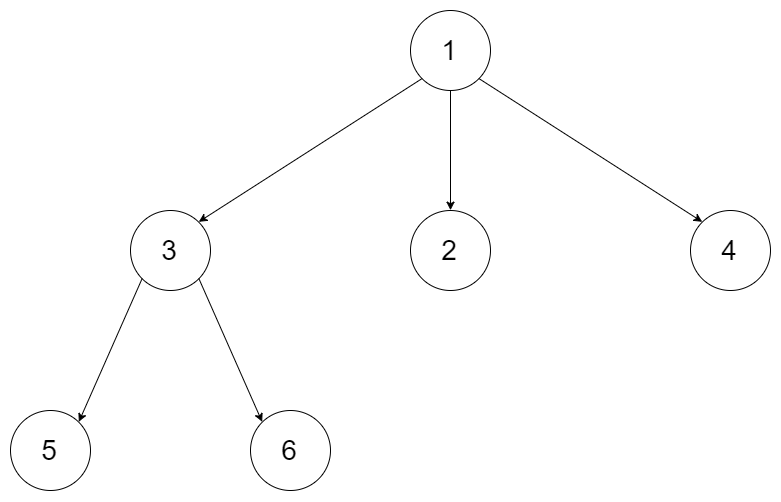 我们应返回其最大深度,3。
我们应返回其最大深度,3。
var maxDepth = function(root) {
if(!root) return 0;
const recursive=(node,depth)=>{
if(!node) return depth;
if(node.children&&node.children.length){
return Math.max(...node.children.map(children=>{
return recursive(children,depth+1);
}))
}
return depth+1;
}
return recursive(root,0);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
# 16、前序遍历(深度优先遍历) 二叉树的直径
示例 :
给定二叉树
1
/
2 3
/ \
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
注意:两结点之间的路径长度是以它们之间边的数目表示。
/**
* @param {TreeNode} root
* @return {number}
*/
//这道题其实是一道求树中最长路径的问题
//而任意一条路径均可以被看作由某个节点为起点,从其左儿子和右儿子向下遍历的路径拼接得到。
var diameterOfBinaryTree = function(root) {
let res=0;
const recursive=node=>{
//该结点不存在,返回0
if(!node) return 0;
const Ldepth=recursive(node.left);
const Rdepth=recursive(node.right);
//获取路径最大值
res=Math.max(res,Ldepth+Rdepth);
//每递归一次,深度+1;
return Math.max(Ldepth,Rdepth)+1;
}
recursive(root);
return res;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 17、前序遍历二叉树中第二小的节点 (opens new window)
给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话,那么该节点的值等于两个子节点中较小的一个。
更正式地说,root.val = min(root.left.val, root.right.val) 总成立。
给出这样的一个二叉树,你需要输出所有节点中的第二小的值。如果第二小的值不存在的话,输出 -1 。
示例 1:
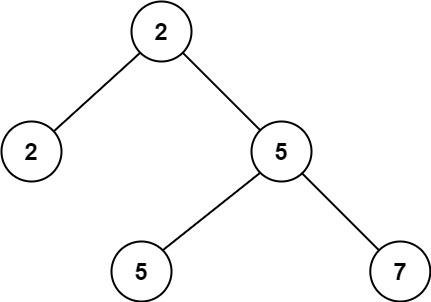 输入:root = [2,2,5,null,null,5,7]
输出:5
解释:最小的值是 2 ,第二小的值是 5 。
输入:root = [2,2,5,null,null,5,7]
输出:5
解释:最小的值是 2 ,第二小的值是 5 。
/**
* @param {TreeNode} root
* @return {number}
*/
//暴力法
var findSecondMinimumValue = function(root) {
const res=new Set();
const recursive=node=>{
if(!node) return;
res.add(node.val);
recursive(node.left);
recursive(node.right);
}
recursive(root);
return [...res].sort((a,b)=>a-b)[1]||-1;
};
//方法 2 找规律
var findSecondMinimumValue = function(root) {
if(!root) return -1;
const recursive=(node,min)=>{
if(!node) return -1;
//根左右 判断当前结点跟最小值的关系
if(node.val>min) return node.val;
//遍历左子树 判断左子节点跟最小值的关系
const left=recursive(node.left,min);
//遍历右子树 判断左子节点跟最小值的关系
const right=recursive(node.right,min);
//没有左子树
if(left===-1) return right;
//没有右子树
if(right===-1) return left;
return Math.min(left,right);
}
return recursive(root,root.val);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 18 、前序遍历 二叉树的堂兄弟节点 (opens new window)
在二叉树中,根节点位于深度 0 处,每个深度为k的节点的子节点位于深度k+1处。如果二叉树的两个节点深度相同,但父节点不同,则它们是一对堂兄弟节点。我们给出了具有唯一值的二叉树的根节点 root,以及树中两个不同节点的值 x 和y。只有与值 x 和 y对应的节点是堂兄弟节点时,才返回 true。否则,返回 false。
输入:root = [1,2,3,null,4,null,5], x = 5, y = 4 输出:true
var isCousins = function(root, x, y) {
/**
* 1、他们父节点不同
* 2、他们的深度一样
*/
//两个对象来存储当前结点的深度和父节点
const depthObj=Object.create(null),parentObj=Object.create(null);
const recursive=(node,parent)=>{
if(!node) return;
depthObj[node.val]=parent?depthObj[parent.val]+1:0;
parentObj[node.val]=parent;
recursive(node.left,node);
recursive(node.right,node);
}
recursive(root,null);
return depthObj[x]===depthObj[y]&&(parentObj[x]!==parentObj[y]);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 19、前序遍历(dfs)求和路径 (opens new window)
给定一棵二叉树,其中每个节点都含有一个整数数值(该值或正或负)。设计一个算法,打印节点数值总和等于某个给定值的所有路径的数量。注意,路径不一定非得从二叉树的根节点或叶节点开始或结束,但是其方向必须向下(只能从父节点指向子节点方向)。 示例: 给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
返回:3 解释:和为 22 的路径有:[5,4,11,2], [5,8,4,5], [4,11,7]
const pathSum=function(root,sum){
if(!root) return 0;
const resolve=(node,target)=>{
if(!node) return 0;
let res=0;
if(node.val===target) return res++;
res+=resolve(node.left,target-node.val);
res+=resolve(node.right,target-node.val);
return res;
}
const dfs=(node,target)=>{
let res=0;
if(!node) return 0;
//深度递归当前结点
res+=resolve(node,target);
//深度递归左结点
res+=dfs(node.left,target);
//深度递归右结点
res+=dfs(node.right,target);
return res;
}
return dfs(root,sum);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 20、修剪二叉搜索树 (opens new window)
给你二叉搜索树的根节点 root ,同时给定最小边界low和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树不应该改变保留在树中的元素的相对结构(即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在唯一的答案。所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
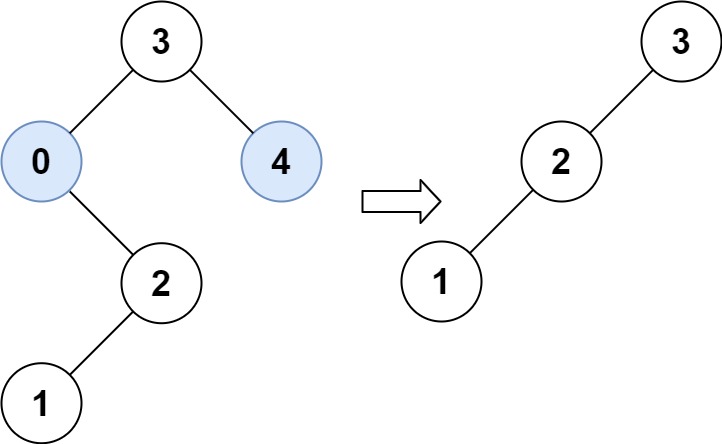 示例 2:
输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出:[3,2,null,1]
示例 2:
输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出:[3,2,null,1]
/**
* @param {TreeNode} root
* @param {number} low
* @param {number} high
* @return {TreeNode}
*/
var trimBST = function(root, low, high) {
//返回当前结点
if(!root) return root;
//当前结点的值大于最大值,那么它右子树上的所有值都会大于当前值,就不用再考虑
if(root.val>high) return trimBST(root.left,low,high);
// //当前结点的值小于最小值,那么它左子树上的所有值都会大于当前值,就不用再考虑
if(root.val<low) return trimBST(root.right,low,high);
//递归当前结点的左子树之后的结果赋值给当前结点的左子树
root.left=trimBST(root.left,low,high);
//递归当前结点的左子树之后的结果赋值给当前结点的左子树
root.right=trimBST(root.right,low,high);
return root;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 24、二叉树的最小深度 (opens new window)
给定一个二叉树,找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 说明:叶子节点是指没有子节点的节点。
//获取树的最小深度
const minDepth=function(root){
if(!root) return 0;
const recur=node=>{
//没有左右节点 则当前节点的深度是1
if(!node.left&&!node.right) return 1;
let minValue=Number.MAX_SAFE_INTEGER;;
if(node.left){
minValue=Math.min(minValue,recur(node.left));
}
if(node.right){
minValue=Math.min(minValue,recur(node.right))
}
return minValue+1;
}
}
//获取树的最大深度
const minDepth=function(root){
if(!root) return 0;
const recur=node=>{
//没有左右节点 则当前节点的深度是1
if(!node.left&&!node.right) return 1;
let maxValue=Number.MIN_SAFE_INTEGER;
if(node.left){
maxValue=Math.max(maxValue,recur(node.left));
}
if(node.right){
maxValue=Math.max(maxValue,recur(node.right))
}
return maxValue+1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
=======
# 21、[后续遍历]好叶子节点对的数量 (opens new window)
给你二叉树的根节点 root 和一个整数 distance 。如果二叉树中两个 叶 节点之间的 最短路径长度 小于或者等于 distance ,那它们就可以构成一组 好叶子节点对 。返回树中 好叶子节点对的数量 。
var countPairs=function(root,distance){
if(!root) return 0;
let res=0;
const dfs=node=>{
// if(!node) return [];
if(!node.left&&!node.right) return [0];
//存放当前结点各叶子结点离它的距离
const leaves=[];
//表示当前结点左结点各叶子结点离它的距离
const leftLeaves=node.left?dfs(node.left):[];
//表示当前结点右结点各叶子结点离它的距离
const rightLeaves=node.right?dfs(node.right):[];
leftLeaves.forEach(leave=>{
++leave<distance&&leaves.push(leave);
})
rightLeaves.forEach(leave=>{
++leave<distance&&leaves.push(leave);
})
//判断当前结点左右结点叶子结点的距离跟distance的关系
for(let i of leftLeaves){
for(let j of rightLeaves){
if(i+j+2<=distance) res+=1;
}
}
return leaves;
}
dfs(root);
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 22、树的子结构 (opens new window)
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构) B是A的子结构, 即 A中有出现和B相同的结构和节点值。
var isSubStructure = function(A, B) {
//前序遍历
const recur=(A,B)=>{
//递归终止条件
//1、遍历到B的叶子结点了,此时B肯定是A的子树
if(!B) return true;
//2、递归A的叶子结点了,但是还没递归到B的叶子结点,或者A,B结点此时都不是叶子结点,但是A的结点的值不等于B的结点的值,那么B不是A的子树
if(!A||A.val!==B.val) return false;
//3、如果A的结点的值不等于B的结点的值,则继续递归遍历
return recur(A.left,B.left)&&recur(A.right,B.right);
}
return Boolean(A&&B)&&(recur(A,B)||isSubStructure(A.left,B)||isSubStructure(A.right,B));
};
2
3
4
5
6
7
8
9
10
11
12
13
# 30、具有所有最深节点的最小子树 (opens new window)
给你一个有根节点的二叉树,找到它最深的叶节点的最近公共祖先。
//深度优先遍历
var lcaDeepestLeaves = function(root) {
const dfs=(node)=>{
if(!node) return new TreeNodeDepth(null,0);
const leftObj=dfs(node.left);
const rightObj=dfs(node.right);
if(leftObj.depth>rightObj.depth){
//左结点对应的深度加1
return new TreeNodeDepth(leftObj.node,leftObj.depth+1);
}
if(leftObj.depth<rightObj.depth){
//右结点的深度加1
return new TreeNodeDepth(rightObj.node,rightObj.depth+1);
}
return new TreeNodeDepth(node,leftObj.depth+1);
}
return dfs(root).node;;
};
function TreeNodeDepth(node,depth){
this.node=node;
this.depth=depth;
console.log(this);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 31、从前序和中序遍历序列构造二叉树 (opens new window)
# 32、将有序数组转换为二叉搜索树 (opens new window)
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
//高度平衡二叉树 即左右子树的结点数差不多;
//所以可以直接取有序数组的中间位置的数作为根节点,开始位置到中间位置的数组的为左子树,中间位置到结束位置的数组为右子树;
var sortedArrayToBST = function(nums) {
const recur=(num,start,end)=>{
if(start>end) return null;
const mid=Math.floor((start+end)/2);
const node=new TreeNode(nums[mid]);
node.left=recur(nums,start,mid-1);
node.right=recur(nums,mid+1,end);
return node;
}
return recur(nums,0,nums.length-1);
};
2
3
4
5
6
7
8
9
10
11
12
13
# 33、二叉树的坡度 (opens new window)
给定一个二叉树,计算 整个树 的坡度 。
一个树的 节点的坡度 定义即为,该节点左子树的节点之和和右子树节点之和的 差的绝对值 。如果没有左子树的话,左子树的节点之和为 0 ;没有右子树的话也是一样。空结点的坡度是 0 。
整个树 的坡度就是其所有节点的坡度之和。
var findTilt = function(root) {
let sum=0;
const recur=(node,parent)=>{
if(!node) return 0;
const leftVal= recur(node.left);
const rightVal=recur(node.right);
sum+=Math.abs(leftVal-rightVal);
//当前结点对应的值=> 左右结点的值+当前结点的值
return leftVal+rightVal+node.val;
}
recur(root);
return sum;
};
2
3
4
5
6
7
8
9
10
11
12
13
# 34、另一颗树的子树 (opens new window)
给定两个非空二叉树 s 和 t,检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。
下面这种情况是不成立的。
给定的树 s:
3
/
4 5
/
1 2
/
0
给定的树 t:
4
/
1 2
返回 false。
var isSubtree = function(s, t) {
const check=(s,t)=>{
//s和t都没有子节点了
if(!t&&!s) return true;
//一个有一个没有,或者两个都有,但是他们的值不等,那么t都不是s的子树
if(!t||!s||t.val!==s.val) return false;
return check(s.left,t.left)&&check(s.right,t.right);
}
const recur=node=>{
if(!node) return false;
let flag;
// //找到一个他们值相同的点
// if(node.val===t.val){
// //判断他们是否相等
// flag =check(node,t);
// }
return check(node,t)|| recur(node.left)||recur(node.right);
};
return recur(s);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20