字符串匹配算法比较多,这里主要总结6种常见的字符串匹配算法。BF算法、RK算法以及BM算法和KMP算法,这4种是单模式串匹配算法;以及Trie树和AC自动机这两种多模式匹配算法。
# 1、单模式匹配算法
# 1、BF算法
BF 算法是 Brute Force 的缩写,中文叫作暴力匹配算法,也叫朴素匹配算法。假如字符串 A是主串,长度是n,字符串B是模式串,长度是m,因为我们在主串中查找模式串,所以n>m。 用一句话概括就是:我们在主串中,检查起始位置分别是 0、1、2…n-m 且长度为 m 的 n-m+1 个子串,看有没有跟模式串匹配的。 BF 算法的时间复杂度很高,是 O(n*m)(遍历n-m+1次,每次都需要比较每个字符,字符长度为m)。
# 2、RK算法——借助哈希算法实现高效字符串匹配。
RK 算法的全称叫 Rabin-Karp 算法。
RK 算法的思路是这样的:我们通过哈希算法对主串中的 n-m+1 个子串分别求哈希值,然后逐个与模式串的哈希值比较大小。如果某个子串的哈希值与模式串相等,那就说明对应的子串和模式串匹配了。
整个RK算法包含两部分,计算子串哈希值和模式串哈希值与子串哈希值的比较。通过扫描一遍主串就可以计算出所有子串的哈希值,这部分的时间复杂度是O(n)。模式串哈希值与每个子串哈希值之间的比较的时间复杂度是 O(1),总共需要比较 n-m+1 个子串的哈希值,所以,这部分的时间复杂度也是 O(n)。所以,RK 算法整体的时间复杂度就是 O(n)。
可以利用二十六进制来计算字符串的哈希值。把a-z这26个字符映射到0-25这26个数字。
"cba"="c"*26^2+"b"*26+"a"*1;=2*26^2+26+1=1353;
当一个子串的哈希值跟模式串相等的时候,比较一下子串和模式串本身就可以了。
RK 算法是借助哈希算法对 BF 算法进行改造,即对每个子串分别求哈希值,然后拿子串的哈希值与模式串的哈希值比较,减少了比较的时间。所以,理想情况下,RK 算法的时间复杂度是 O(n)。
# 3、BM算法——实现文本编辑器中的查找功能
BM(Boyer-Moore)算法是一种非常高效的字符串匹配算法,根据实验统计,它的性能是著名的KMP算法的3到4倍。
BM(Boyer-Moore)算法的核心思想。就是在模式串和主串不匹配的时候,能够跳过一些肯定不会匹配的情况时,将模式串往后多滑动几位。
# 1、BM算法原理分析
BM 算法包含两部分,分别是坏字符规则 (bad character rule) 和好后缀规则 (good suffix shift)。
# 1、坏字符规则
我们从模式串的末尾往前倒着匹配,当我们发现某个字符没法匹配的时候。我们把这个没有匹配的字符叫作坏字符(主串中的字符)。
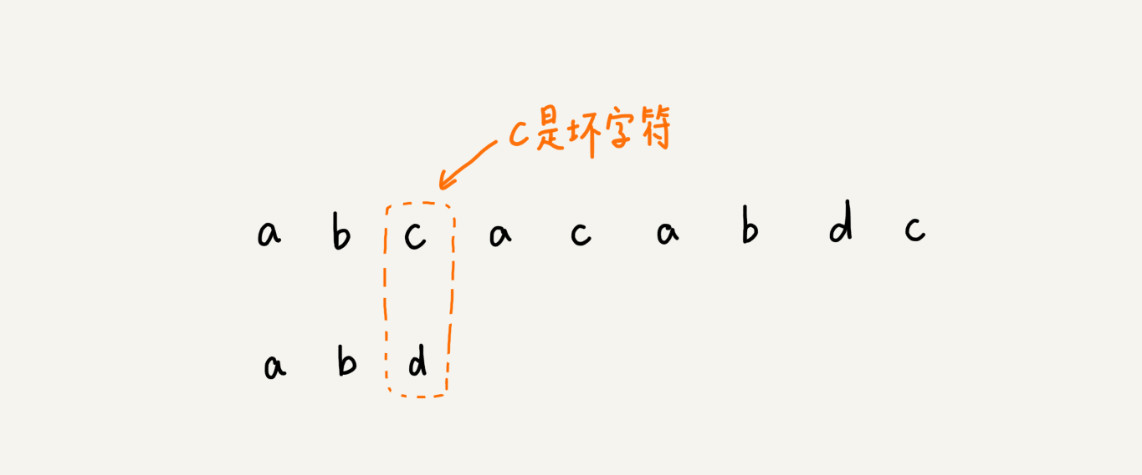
当发生不匹配的时候,我们把坏字符对应的模式串中的字符下标记作 si。如果坏字符在模式串中存在,我们把这个坏字符在模式串中的下标记作 xi。如果不存在,我们把 xi 记作 -1。那模式串往后移动的位数就等于 si-xi。(注意,我这里说的下标,都是字符在模式串的下标)。
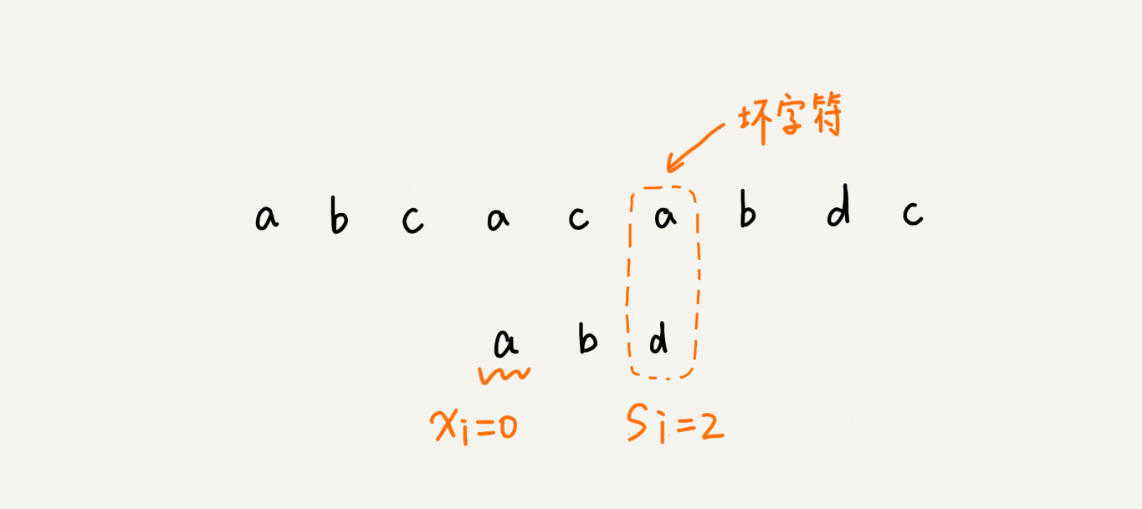
如果坏字符在模式串里多处出现,那我们在计算 xi 的时候,选择最靠后的那个,因为这样不会让模式串滑动过多,导致本来可能匹配的情况被滑动略过。
利用坏字符规则,BM 算法在最好情况下的时间复杂度非常低,是 O(n/m)。比如,主串是 aaabaaabaaabaaab,模式串是 aaaa。每次比对,模式串都可以直接后移四位。
单纯使用坏字符规则还是不够的。因为根据 si-xi 计算出来的移动位数,有可能是负数,比如主串是 aaaaaaaaaaaaaaaa,模式串是 baaa。不但不会向后滑动模式串,还有可能倒退。si=0,xi=1,向后滑动一位,所以BM算法还需要用到好后缀规则。
# 2、好字符规则
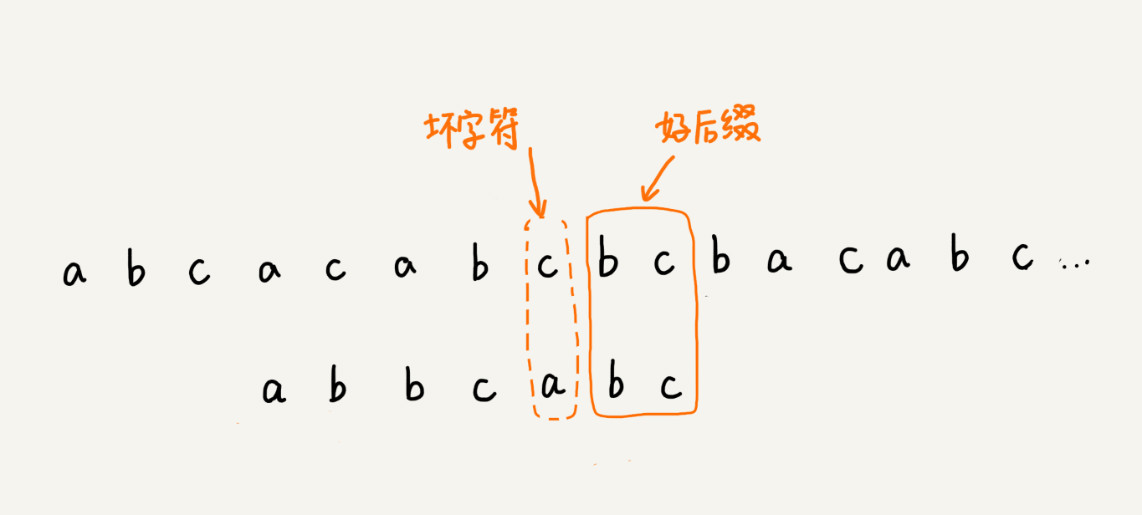
我们把已经匹配的 bc 叫作好后缀,记作 {u}。我们拿它在模式串中查找,如果找到了另一个跟 {u} 相匹配的子串 {u*},那我们就将模式串滑动到子串 {u*}与主串中 {u}对齐的位置。 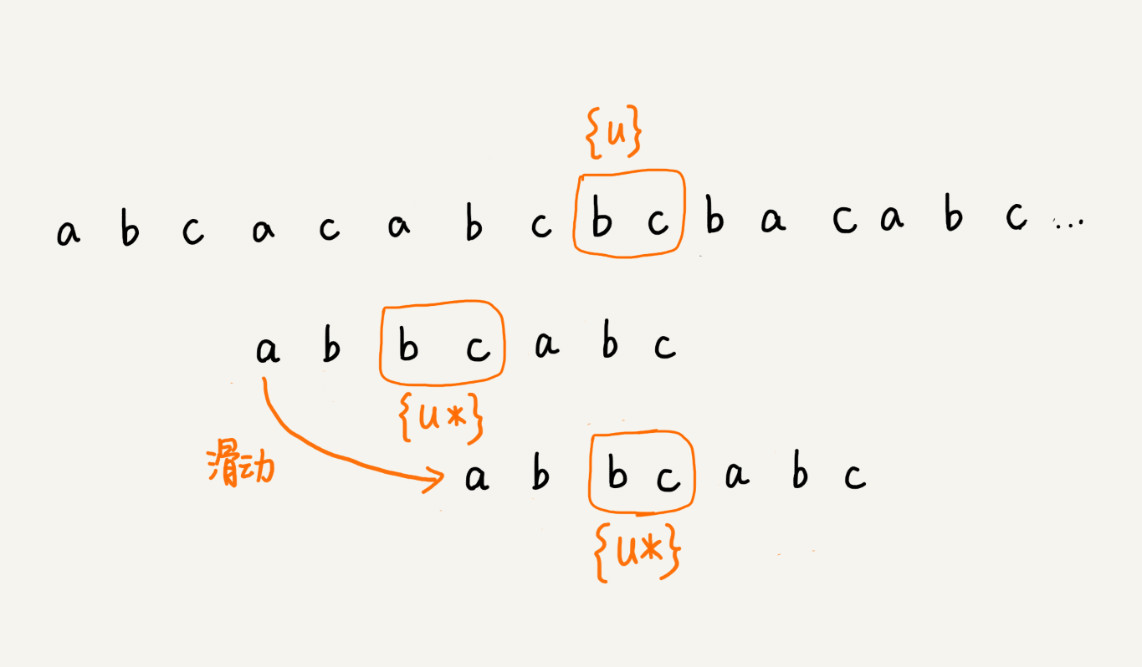
如果在模式串中找不到另一个等于 {u} 的子串,我们就直接将模式串,滑动到主串中{u}的后面,因为之前的任何一次往后滑动,都没有匹配主串中 {u} 的情况。
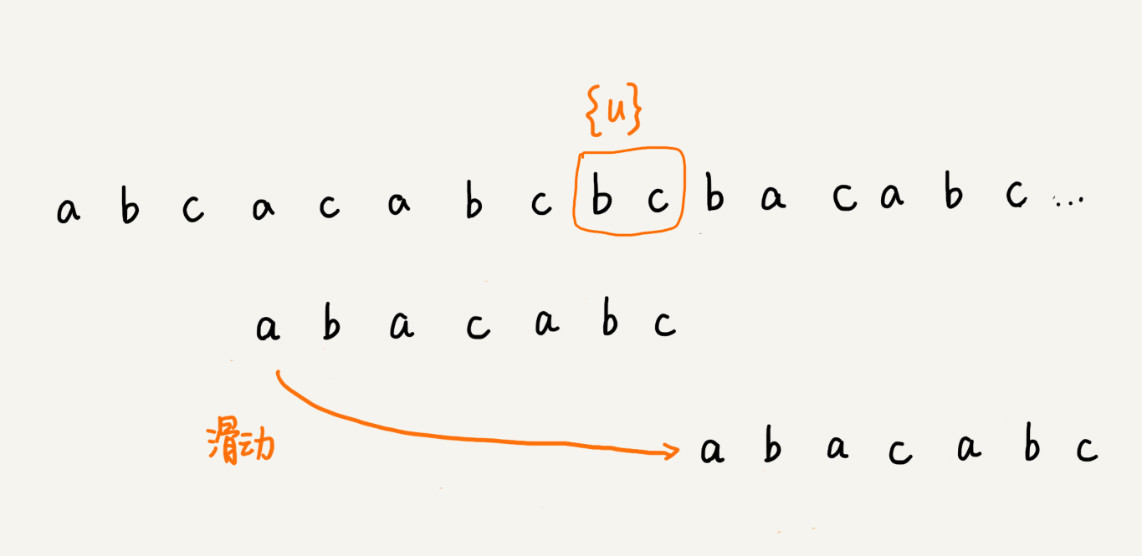
当模式串滑动到前缀与主串中 {u} 的后缀有部分重合的时候,并且重合的部分相等的时候,就有可能会存在完全匹配的情况。针对这种情况,我们不仅要看好后缀在模式串中,是否有另一个匹配的子串,我们还要考察好后缀的后缀子串,是否存在跟模式串的前缀子串匹配的。
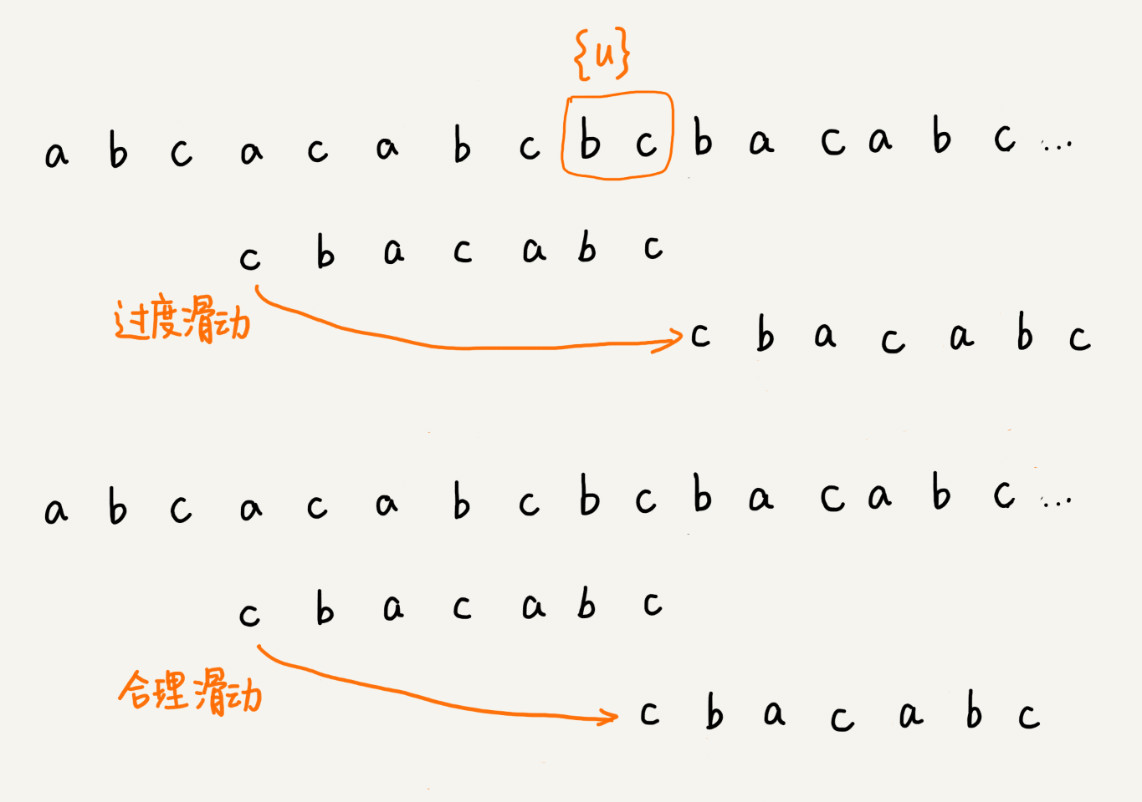
字符串 s 的后缀子串,就是最后一个字符跟 s 对齐的子串,比如 abc 的后缀子串就包括 c, bc。所谓前缀子串,就是起始字符跟 s 对齐的子串,比如 abc 的前缀子串有 a,ab。我们从好后缀的后缀子串中,找一个最长的并且能跟模式串的前缀子串匹配的,假设是{v},然后将模式串滑动到如图所示的位置。
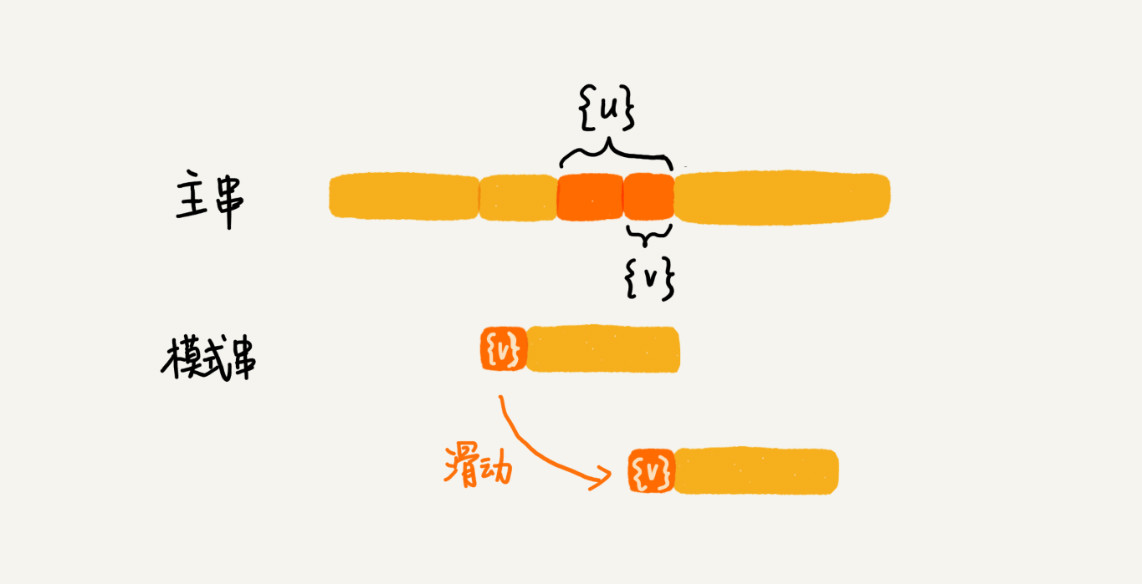
当模式串和主串中的某个字符不匹配的时候,如何选择用好后缀规则还是坏字符规则,来计算模式串往后滑动的位数? 我们可以分别计算好后缀和坏字符往后滑动的位数,然后取两个数中最大的,作为模式串往后滑动的位数。这种处理方法还可以避免我们前面提到的,根据坏字符规则,计算得到的往后滑动的位数,有可能是负数的情况。
# 3、BM算法代码实现
可以将模式串中的每个字符及其下标都存到散列表中。这样就可以快速找到坏字符在模式串的位置下标了。我们用大小为 256 的数组,来记录每个字符在模式串中出现的位置。数组的下标对应字符的 ASCII 码值,数组中存储这个字符在模式串中出现的位置。
/**
*
* @param {String} b 模式串
* @param {Number} m 模式串的长度
* @return {*} bc 散列表
*/
function generateBC(b,m,bc){
const bc=new Array(m).fill(-1);
for(let i=0;i<m;i++){
const ascii=b[i].charCodeAt();
bc[ascii]=i;
}
return bc;
}
/**
* 坏字符规则的框架代码
* @param {String} a 主串
* @param {Number} n 主串的长度
* @param {String} b 模式串
* @param {Number} m 模式串的长度
*/
function bm(a,n,b,m){
const bc=new Array(256);
generateBC(b,m,bc);//构建换字符哈希表
let i=0;//i表示住串与模式串对齐的第一个字符
while(i<=n-m){
let j;
for(j=m-1;j>=0;j--){ //模式串从后往前匹配
if(a[i+j]!==b[j]) break;
}
if(j<0) return i;//匹配成功,返回主串和模式串第一个匹配的位置
//等同于将模式串往后滑动j-bc[a[i+j]]位
//bc[a[i+j].charCodeAt()]表示坏字符在模式串中的索引
i=i+(j-bc[a[i+j].charCodeAt()]);
}
return -1
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
suffix数组: suffix 数组的下标 k,表示后缀子串的长度,下标对应的数组值存储的是,在模式串中跟好后缀 {u} 相匹配的子串 {u*} 的起始下标值。
prefix数组: 用于记录模式串的后缀子串是否能匹配模式串的前缀子串。
如何来填充这两个数组的值?

分析:后缀子串在整个模式串中的索引是 suffix[i]=s.slice(0,-1).indexof(后缀子串)的值;prefix[i]表示suffix[i]在前缀子串中的索引值是否等于0。 cabcab的前缀子串有a,ca,cab,cabc,cabca
//用于计算好好后缀规则
function generateGS(b,m){
const suffix=new Array(m).fill(-1);
const prefix=new Array(m).fill(false);
for(let i=0;i<m-1;i++){
let j=i,k=0;//k表示公共后缀子串长度
while(j>=0&&b[j]==b[m-i-k]){
--j;
++k;
suffix[k]=j+1;//j+1表示公共后缀子串在b[0,i]中的起始下标
}
if(j===-1) prefix[k]=true;//表示公共后缀子串也是模式串的前缀子串
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
BM算法的完整版代码实现如下所示:
function bm(a,b){
const n=a.length,m=b.length;
const bc=generateBC(b,m);
const suffix=new Array(m).fill(-1);
const prefix=new Array(m).fill(false);
generateGS(b,m,suffix,prefix);
let i=0;//j表示主串跟模式串匹配的第一个字符
while(i<=n<m){
let j;
for(j=m-1;j>=0;j--){//模式串从后往前匹配
if(a[i+j]!==b[j]) break;//坏字符对应模式中的下标是将j
}
if(j<0) return i;//匹配成功,返回主串跟模式串第一个匹配的字符的位置
let x=j-bc[a[i+j].charCodeAt()];//表示移动的位数
let y=0;
//表示找到了
if(j<m-1){
y=moveByGS(j,m,suffix,prefix);
}
i=i+Math.max(x,y);//表示移动的位数
}
return -1
}
//bc表示字符的编码值在模式串中的索引
function generateBC(b,m){
const bc=new Array(m).fill(-1);
for(let i=0;i<m;i++){
const ascii=b[i].charCodeAt();
bc[ascii]=i;
}
return bc;
}
//判断后缀子串跟前缀子串是否有相等的情况
function generateGS(b,m,suffix,prefix){
for(let i=0;i<m-1;i++){
let j=i,k=0;//k表示公共后缀子串长度
while(j>=0&&b[j]==b[m-i-k]){
--j;
++k;
suffix[k]=j+1;//j+1表示公共后缀子串在b[0,i]中的起始下标
}
if(j===-1) prefix[k]=true;//表示公共后缀子串也是模式串的前缀子串
}
}
//在模式串跟主串匹配的过程中,遇到不能匹配的字符时,如何根据好后缀规则,计算模式串往后滑动的位数?
function moveByGS(j,m,suffix,prefix){
//j表示坏字符对应的模式串中的字符下标
//j+1表示好后缀开始的位置
let k=m-(1+j);//好后缀长度
//1、表示好后缀子串跟前缀子串有相等的情况
if(suffix[k]!==-1) return j-suffix[k]+1;//表示移动的位数
//j是坏字符,j+1是好后缀开始字符,好后缀的子后缀是不包括第一位的,所以从j+2开始
//2、遍历好后缀的后缀子串
for(let r=j+2;r<=m-1;r++){
if(prefix[m-r]){
return r;
}
}
// 前面两条规则都没有找到可以匹配好后缀及其后缀子串的子串,则将整个模式串后移m位
return m;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
总结: BM 算法核心思想是,利用模式串本身的特点,在模式串中某个字符与主串不能匹配的时候,将模式串往后多滑动几位,以此来减少不必要的字符比较,提高匹配的效率。BM 算法构建的规则有两类,坏字符规则和好后缀规则。好后缀规则可以独立于坏字符规则使用。因为坏字符规则的实现比较耗内存,为了节省内存,我们可以只用好后缀规则来实现 BM 算法。
# 4、KMP算法——好前缀规则
KMP算法的核心思想,跟BM算法非常相近。这里我们类比一下,在模式串和主串匹配的过程中,我们把能匹配的那个字符仍然叫做坏字符,把已经匹配的那段字符叫做好前缀。
当遇到坏字符的时候,就把模式串往后滑动,在滑动的过程中,只要模式串和好前缀有上下重合,前面几个字符的比较,就相当于拿好前缀的后缀子串,跟模式串的前缀子串在比较。
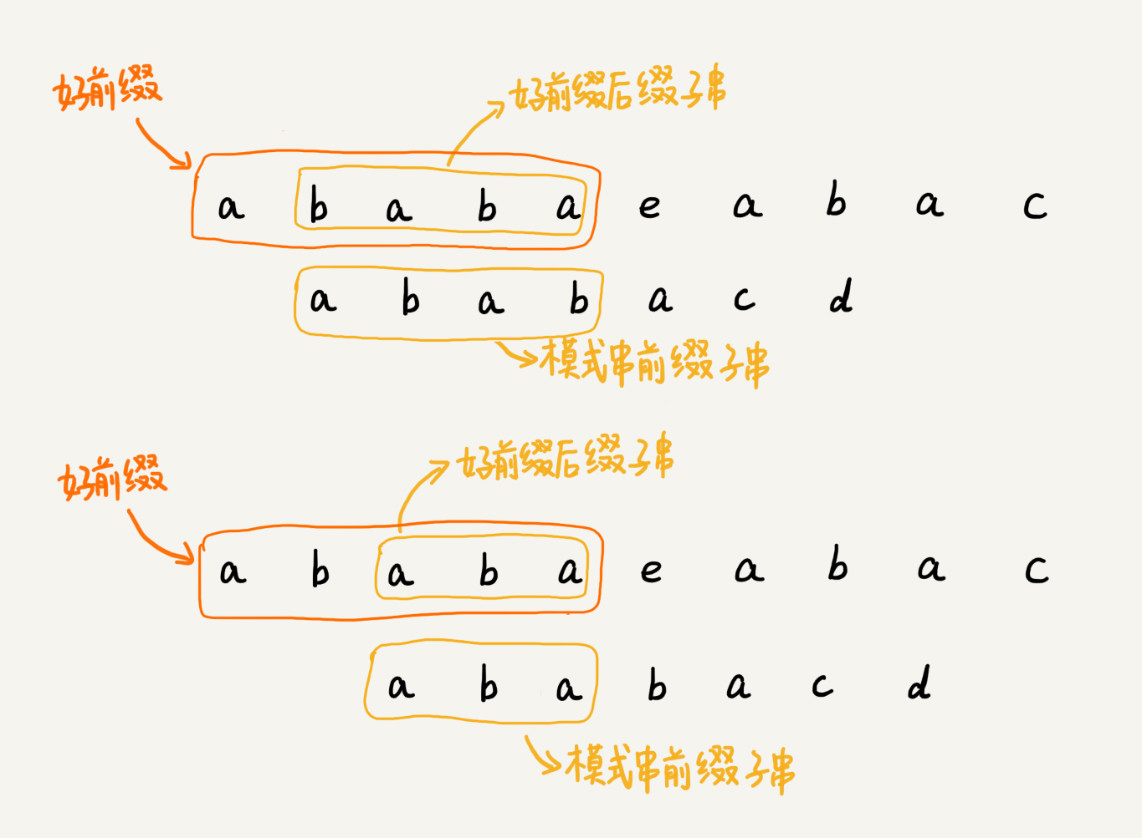
拿好前缀本身,在它的后缀子串中,查找最长的那个可以跟好前缀的前缀子串匹配的。假设最长的可匹配的那部分前缀子串是 {v},长度是 k。我们把模式串一次性往后滑动 j-k 位,相当于,每次遇到坏字符的时候,我们就把 j 更新为 k,i 不变,然后继续比较。

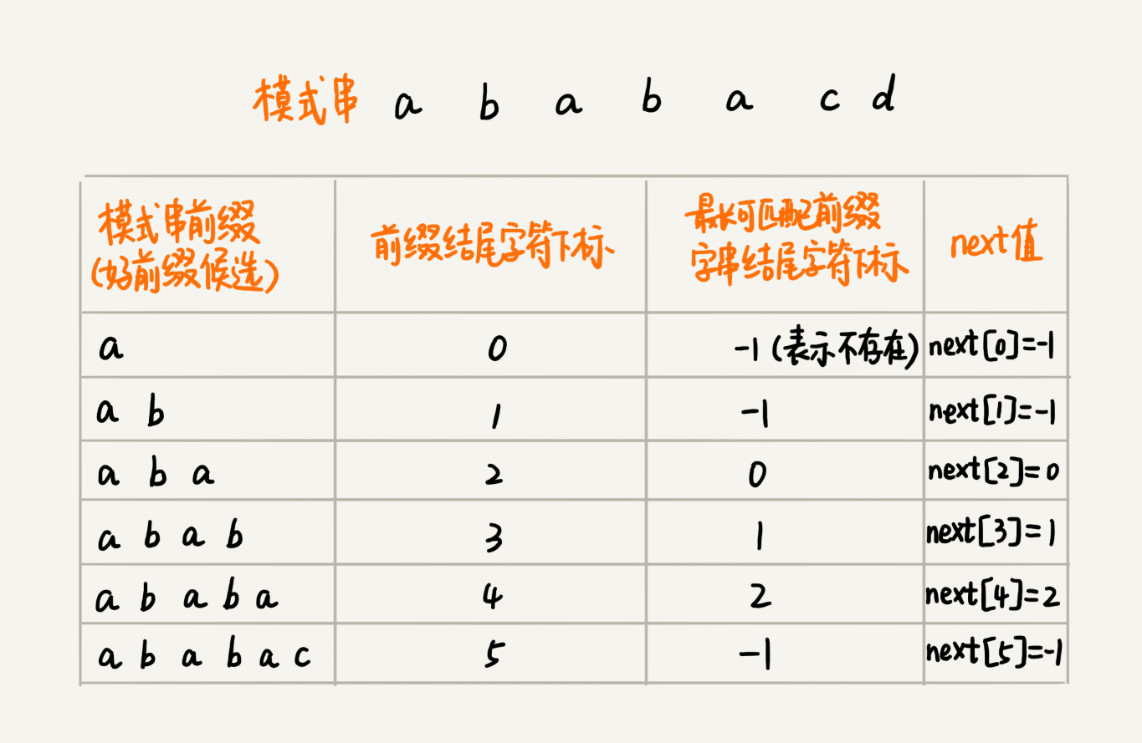
把好前缀的所有后缀子串中,最长的可匹配前缀子串的那个后缀子串,叫作最长可匹配后缀子串;对应的前缀子串,叫作最长可匹配前缀子串。

KMP 算法提前构建一个数组,用来存储模式串中每个前缀(这些前缀都有可能是好前缀)的最长可匹配前缀子串的结尾字符下标。我们把这个数组定义为 next 数组,很多书中还给这个数组起了一个名字,叫失效函数(failure function)。
数组的下标是每个前缀结尾字符下标,数组的值是这个前缀的最长可以匹配前缀子串的结尾字符下标。
KMP算法的框架代码
function kmp(a,b){
const n=a.length,m=b.length;
const next=getNexts(b,m);
let j=0;
for(let i=0;i<n;i++){
//j指示着当前的坏字符
//j-1是好前缀结尾字符的下标,next[j-1]是好前缀的最长可匹配前缀子串的结尾字符的下标。
while(j>0&&a[i]!==b[j]){
//j重置
j=next[j-1]+1;
}
//字符相等
if(a[i]===b[j]){
j++;
}
if(j===m){ //找到匹配模式串的了
return i-m+1;
}
}
return -1;
}
//计算next数组 预处理
function getNexts(b,m){
const next=new Array(m);
next[0]=-1;
let k=-1;
for(let i=1;i<m;i++){
//当模式串的子串长度后移一位,那么就要判断之前最长可匹配前缀子串的下标加1对应的字符和最后一位字符是否相等,如果不相等,就判断后移一位之前最长可匹配前缀子串的最长可匹配前缀的下标加1是否和最后一位字符相等,直到k=-1。
//k肯定是小于i的
while(k!=-1&&b[k+1]!==b[i]){
//本质上是在减少k的值
//表示后移一位之前最长可匹配前缀子串的最长可匹配前缀子串的下标
k=next[k];
}
//相等的情况下,往后移一位,继续比较
if(b[k+1]===b[i]){
k++;
}
next[i]=k;
}
return next;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# 1、KMP 算法复杂度分析
# getNexts中的复杂度分析:
KMP 算法只需要一个额外的 next 数组,数组的大小跟模式串相同。所以空间复杂度是 O(m),m 表示模式串的长度。for循环的时间复杂度是m,而for循环内部的 while循环实际上是在减小k的值,k累积都没有超过m,所以while循环里面的k=next[k]总的执行次数也不可能超过m。 next 数组计算的时间复杂度是O(m)。
# kmp中复杂度分析:
for循环的时间复杂度是O(n),while循环实际上也是在减小j的值,而j总共增长的量都不会超过n,那减少的量也不可能超过n,所以while循环中的这条语句的执行次数也不会超过n,所以这部分的时间复杂度是O(n)。
所以,KMP的时间复杂度是O(n+m)。
# 2、多模式匹配算法
# 1、Trie树——实现搜索引擎的搜索关键词提示功能
也叫字典树,是一种专门处理字符串匹配的数据结构,用来解决在一组字符集合中快速查找某个字符串的问题。 Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起。 每个节点表示一个字符串中的字符,从根节点到红色节点的一条路径表示一个字符串(注意:红色节点并不都是叶子节点)。
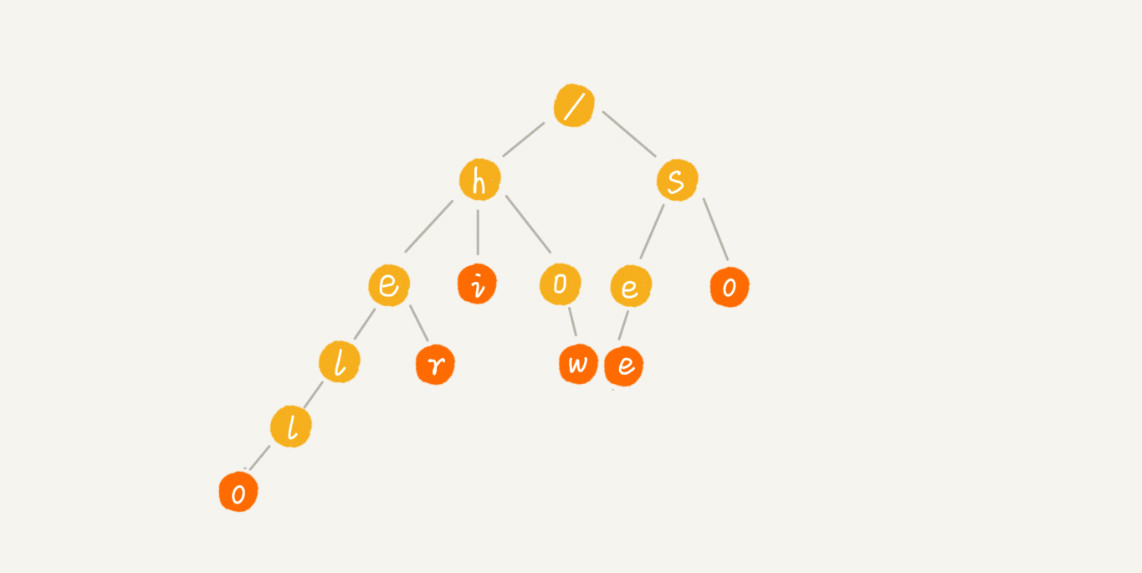
# 1、如何实现一棵Trie树?
Trie 树主要有两个操作,一个是将字符串集合构造成 Trie 树,就是一个将字符串插入到 Trie 树的过程。另一个是在 Trie 树中查询一个字符串。
假设我们的字符串中只有从 a 到 z 这 26 个小写字母,我们在数组中下标为 0 的位置,存储指向子节点 a 的指针,下标为 1 的位置存储指向子节点 b 的指针,以此类推,下标为 25 的位置,存储的是指向的子节点 z 的指针。如果某个字符的子节点不存在,我们就在对应的下标的位置存储 null。
Trie的源码实现
class TrieNode {
constructor(data){
this.data = data;
this.children = new Array(26);
this.isEndingChar = false
}
}
class TrieTree{
static startCode="a".charCodeAt();
constructor(){
this.root=new TrieNode("/");
}
insert(text){
let node=this.root;
const startCode=TrieTree.startCode;
for(let char of text){
const index=char.charCodeAt()-startCode;
//没有找到则添加
if(!node.children[index]){
node.children[index]=new TrieNode(char);
}
node=node.children[index];
}
node.isEndingChar=true;
}
//查找是否含有某个字符串
find(text){
let node=this.root;
const startCode=TrieTree.startCode;
for(let char of text){
const index=char.charCodeAt()-startCode;
//找到了则继续找它的子节点
if(node.children[index]){
node=node.children[index];
}else{
//没有找到
return false
}
}
return node.isEndingChar;
}
//判断是否是以某个字符串开始
startsWith(text){
let node=this.root;
const startCode=TrieTree.startCode;
for(let char of text){
const index=char.charCodeAt()-startCode;
//找到了则继续找它的子节点
if(node.children[index]){
node=node.children[index];
}else{
//没有找到
return false
}
}
return true
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
Trie 树最有优势的是查找前缀匹配的字符串,比如搜索引擎中的关键词提示功能这个场景。
# 2、AC自动机
← 数据结构之堆 数据结构之树的基础知识 →