# 1、什么是堆?
堆是一种特殊的树,树只要满足了以下两点,就是一个堆。
- 堆是一个完全二叉树。
- 堆中每一个节点的值都必须大于等于(或小于等于)其左右节点的值。
完全二叉树就是除了最后一层,其他层的节点个数都是满的,最后一层的节点都靠左排列。
完全二叉树比较适合用数组来存储。因为我们不需要存储左右子节点的指针,单纯的通过数组的下标,就可以找到一个节点的左右子节点和父节点。(图片来源于网络)
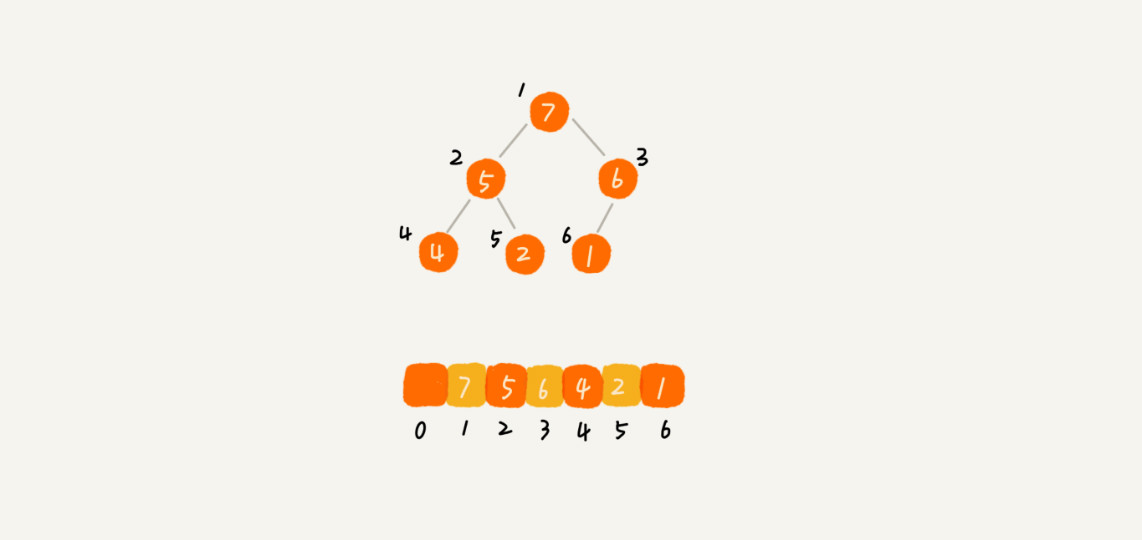
从图中我们可以看出数组中下标为 i 的左子节点,就是下标为 i*2 的节点,右子节点就是下标为 i*2+1的节点,父节点就是Math.floor(i/2)的节点。z
堆化实际上有两种,从下往上和从上往下。这里我先讲从下往上的堆化方法。
# 2、往堆中插入一个元素(从下往上的堆化方法)
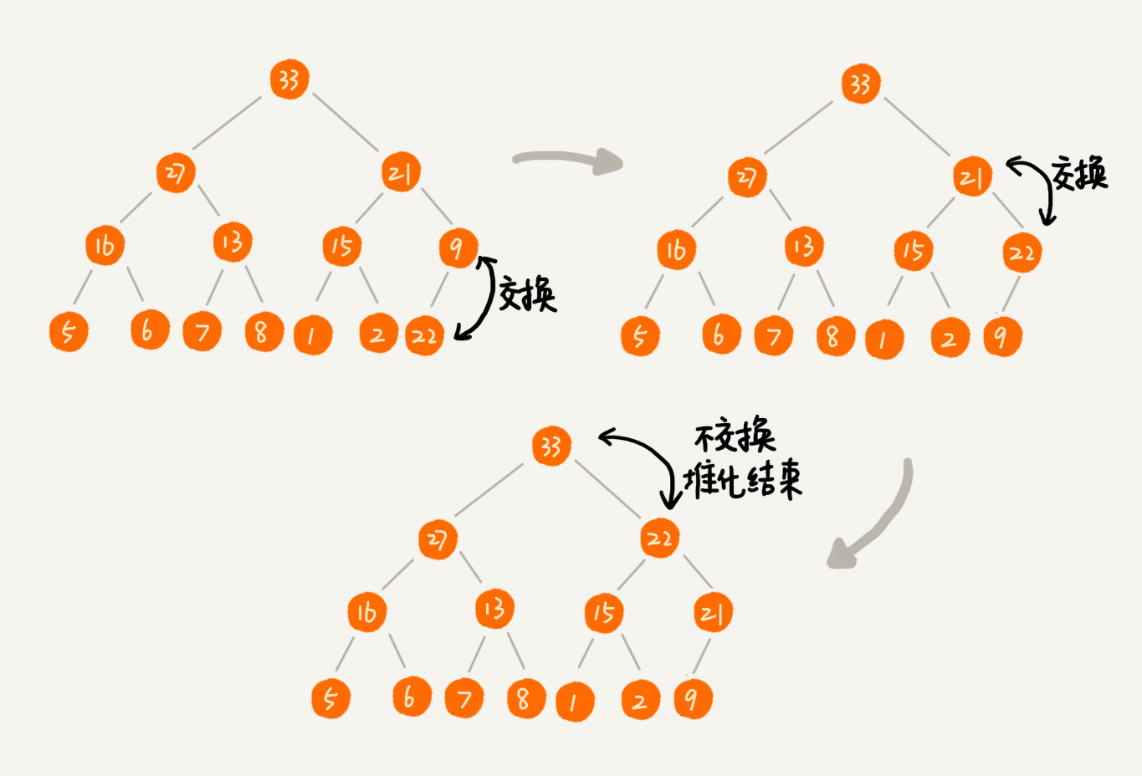
往堆中插入一个元素时,我们需要不断的调整,让其重新满足堆的特性。堆化操作就是顺着节点所在的路径,向上或者向下,对比,然后交换。 堆化有两种,从下往上和从上往下。
//大顶堆
function insert(arr,data) {
arr.push(data);
let i = arr.length-1,tempIndex; //最后一个非叶子结点的索引值
// 自下往上堆化 比较父子节点的大小关系
while ((tempIndex=Math.floor(i / 2)-1) >= 0 && arr[i] > arr[tempIndex]) {
// swap()函数作用:交换下标为i和i/2的两个元素
[arr[i],arr[tempIndex]]=[arr[tempIndex],arr[i]];
i = tempIndex;
}
console.log(arr);//[8, 6, 7, 3, 2, 1, 5]
}
insert([7,6,5,3,2,1],8);
2
3
4
5
6
7
8
9
10
11
12
13
14
# 3、删除堆顶元素(从上往下的堆化方法)
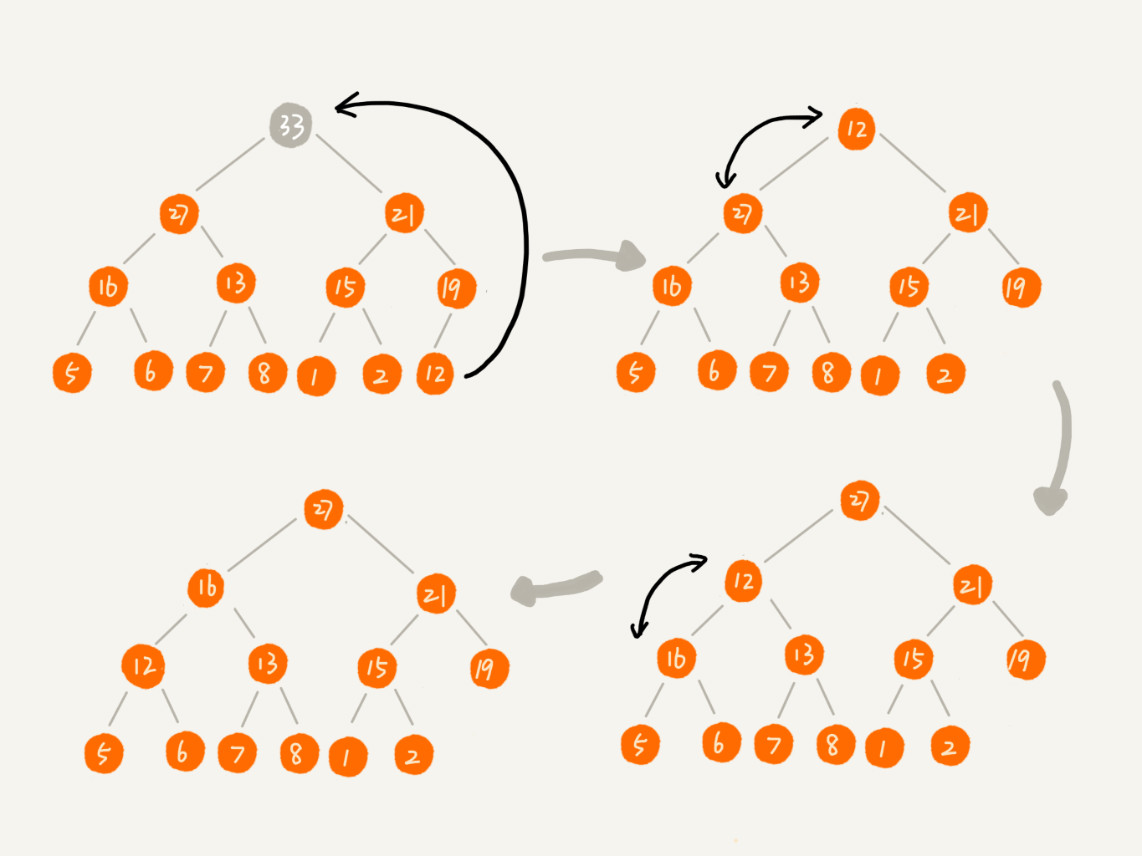
将最后一个结点放到堆顶然后利用同样的父子节点对比方法。对于不满足父子节点大小关系的,互换两个节点,并且重复这个过程,直到父子节点满足大小关系为止。这就是从上往下的堆化方法。因为我们移除的是数组中的最后一个元素,而在堆化的过程中,都是交换操作,不会出现数组中的“空洞”,这种方法堆化之后的结果,满足完全二叉树的特性。
function removeMax(arr) {
arr[0]=arr.splice(arr.length-1,1)[0];
let i=0,n=arr.length;
// 自上往下堆化
while (true) {
let maxPos = i;
if (i*2+1 <= n && arr[i] < arr[i*2+1]) maxPos = i*2+1;
if (i*2+2 <= n && arr[maxPos] < arr[i*2+2]) maxPos = i*2+2;
if (maxPos == i) break;
[arr[i],arr[maxPos]]=[arr[maxPos],arr[i]]
i = maxPos;
}
console.log(arr);//[6, 3, 5, 1, 2]
}
removeMax([7,6,5,3,2,1])
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 4、堆排序
借助于堆这种数据结构实现的排序算法,就叫做堆排序。这种排序方法的时间复杂度非常稳定,是 O(nlogn),并且它还是原地排序算法。 把堆排序的过程大致分解成两个大的步骤,建堆和排序。
# 1、建堆
建堆的过程,有两种思路。
- 第一种,就是前面说过的,在堆中插入一个元素的思路。从前往后插入数据,并且每个数据插入堆中时,都是从下往上堆化。起初堆中只包含一个数据,调用前面的插入操作,将数组后面的数据依次插入到堆中,这样就完成的数组的堆化。
- 第二种,从后往前处理数组数据,并且每个数据插入堆中时,都是从上往下堆化。因为叶子结点往下堆化只能自己跟自己比较,所以从最后一个非叶子结点开始,依次堆化就行了。如下图所示(图片来源于网络)
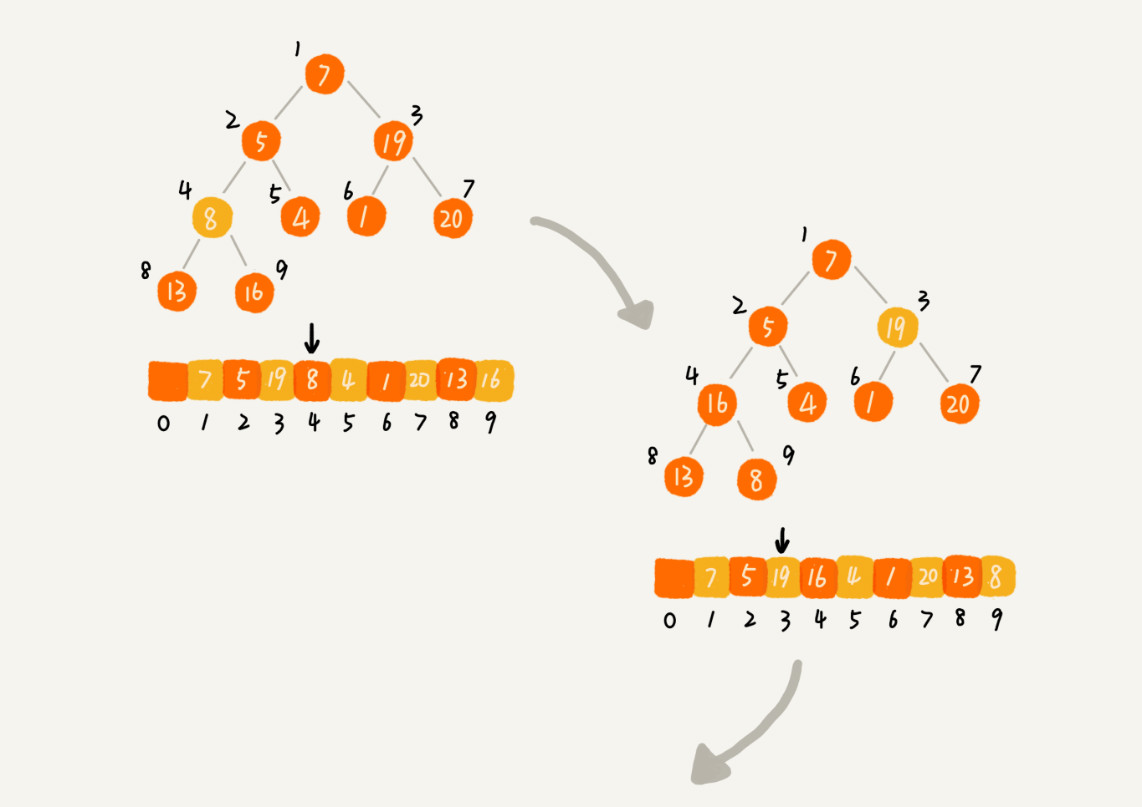
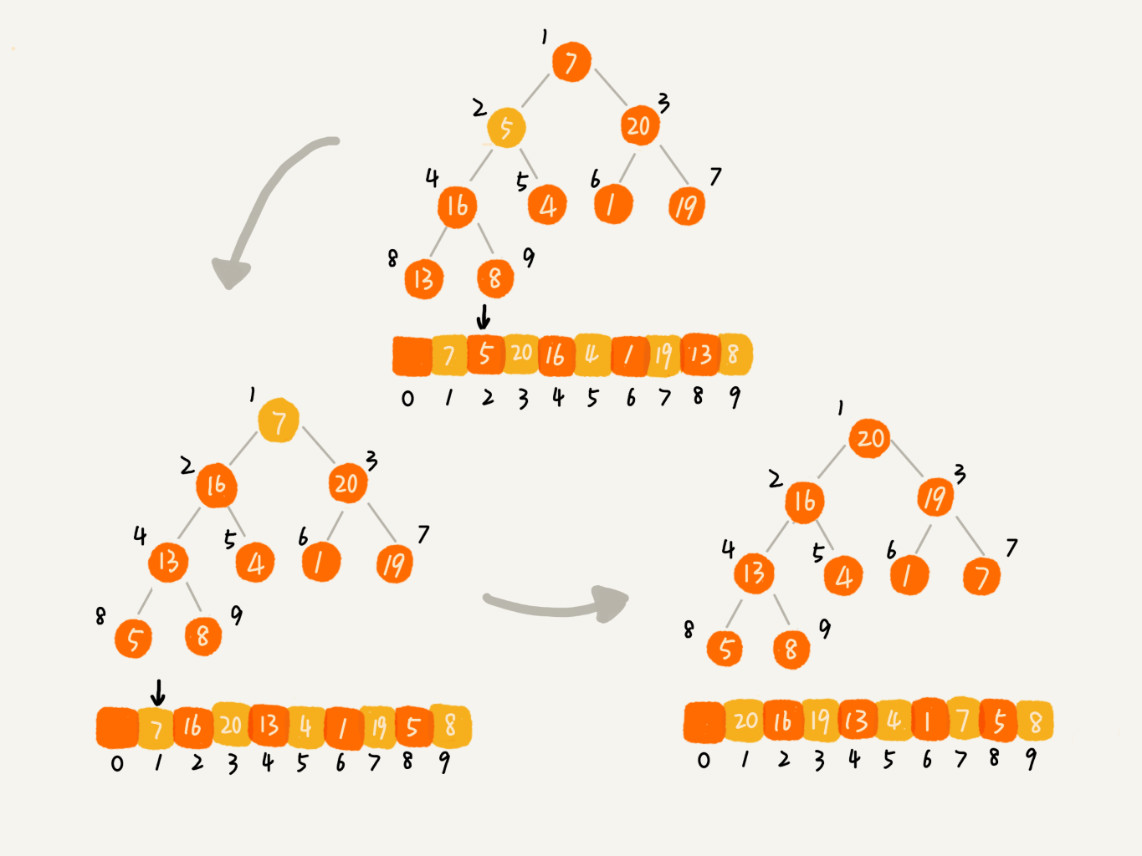
代码实现如下
function buildHeap (arr) {
const len = arr.length;
//最后一个非叶子节点的索引
let i = Math.floor(len / 2)-1;
for (; i >= 0; i--) {
heapify(arr, len-1, i)
}
}
function heapify (arr, n, i) {
while (true) {
let maxPos = i;
if (i * 2 + 1 <= n && arr[i] < arr[i * 2 + 1]) maxPos = i * 2 + 1;
if (i * 2 + 2 <= n && arr[maxPos] < arr[i * 2 + 2]) maxPos = i * 2 + 2;
if (maxPos == i) break;
//交换位置
[arr[i], arr[maxPos]] = [arr[maxPos], arr[i]]
i = maxPos;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
建堆的时间复杂度分析。 因为叶子节点不需要堆化,所以需要堆化的节点从倒数第二层开始,每个节点堆化的过程中,需要比较和交换的节点个数,跟这个节点的高度 k 成正比。将每个节点的高度求和,得到的就是建堆的时间复杂度。
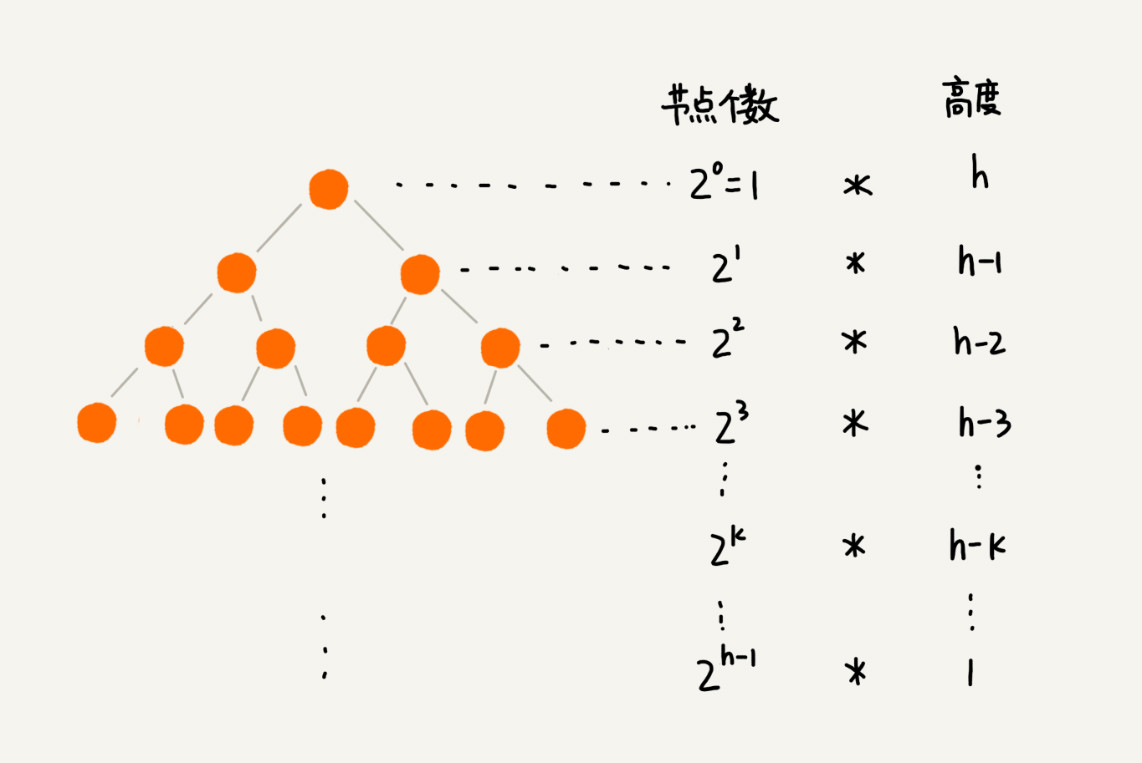
将每个非叶子节点的高度求和,得到公式:
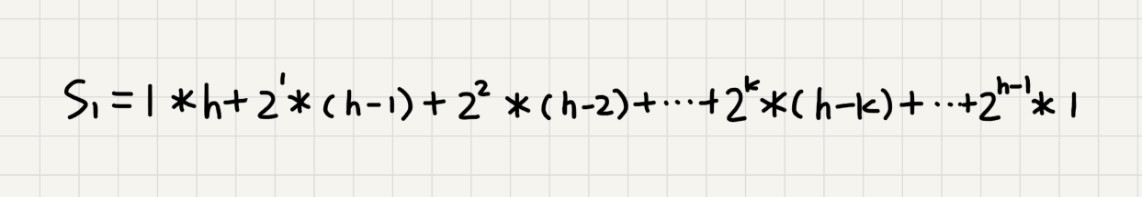 根据错位相减法,可以得到下面的公式:
根据错位相减法,可以得到下面的公式:

根据等比数列求和的公司来计算,可以得到最终的结果:
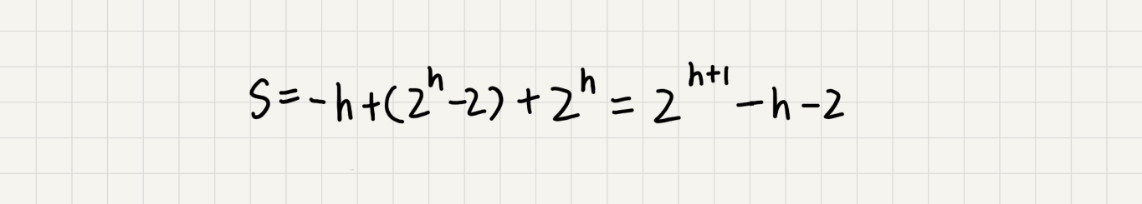
因为h=Math.log2(n),代入公式S,可以得到S=O(n),所以建堆的时间复杂度就是O(n)。
# 2、排序
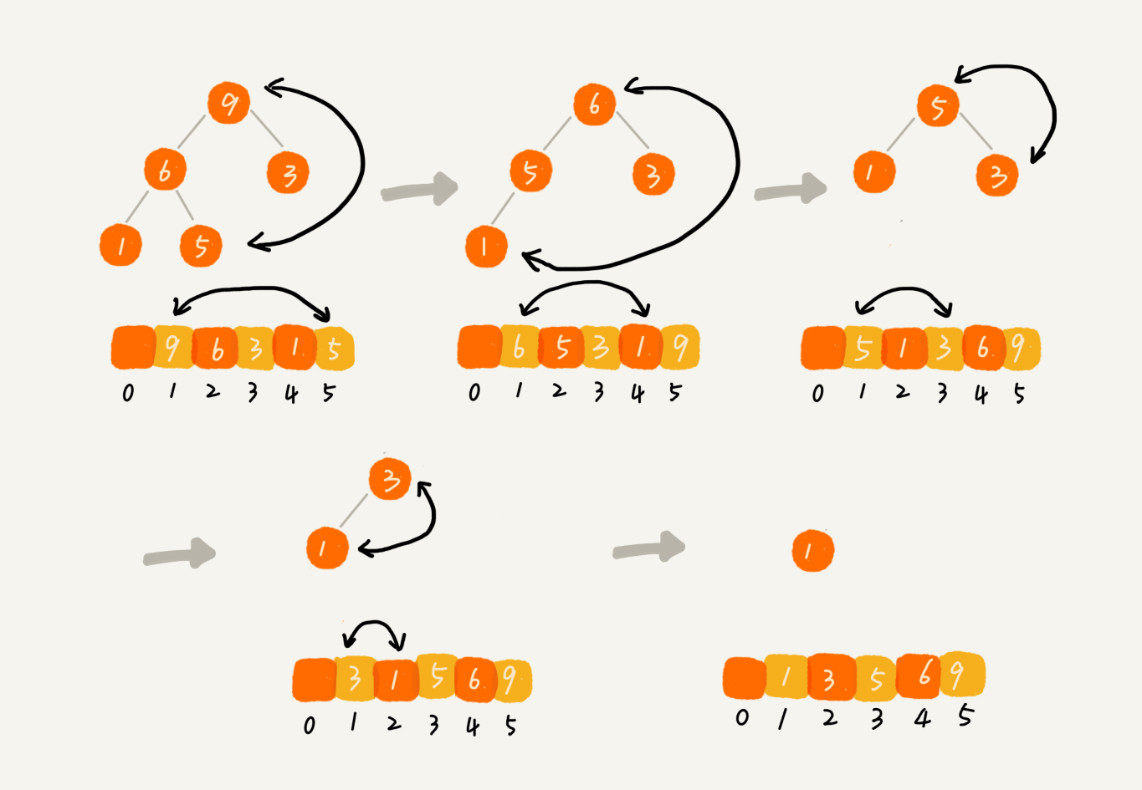
建堆结束后,数组中的数据是按照大顶堆的特性来组织的。数组中的第一个元素就是堆顶,也就是最大的元素。我们将它跟最后一个元素交换,那最大元素就放到了下标为n的位置。(数组的长度为n)。这个过程就是不断删除堆顶元素 的操作,直到队中只剩下最后一个元素,那么就对数组元素排好了序。
function heapSort(arr){
buildHeap(arr);
let len=arr.length-1;
while(len>0){
//将堆顶元素放到最后排好序的数组的首位
[arr[0],arr[len]]=[arr[len],arr[0]];
len--;
//将最大元素调整到堆顶
heapify(arr,len,0)
}
console.log("排好序的数据",arr);
}
2
3
4
5
6
7
8
9
10
11
12
分析:整个堆排序的过程,都只需要个别临时存储空间,所以对排序是原地排序算法。堆排序包括建堆和排序两个操作,建堆的时间复杂度是O(n),排序的过程的时间复杂度是O(nlog(n)),所以对排序整体的时间复杂度是O(nlog(n))。堆排序不是稳定的排序算法,在排序的过程中,存在将堆的最后一个节点跟堆顶节点互换的操作,所以就有可能改变数值相同数据的原始相对排序。
# 5、快速排序的性能比堆排序好的原因所在?
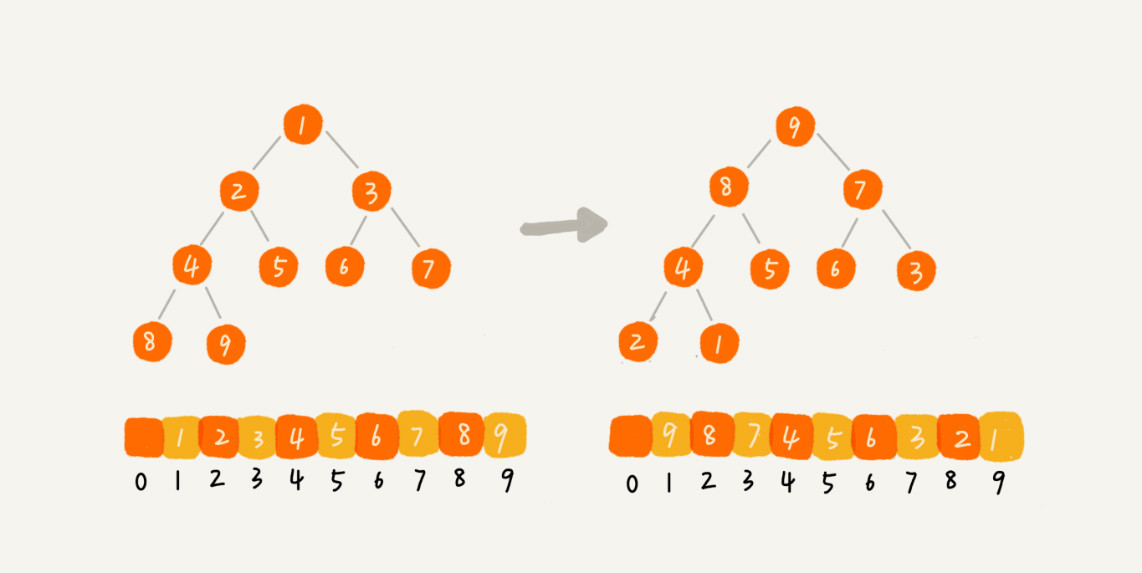
- 堆排序数据访问的方式没有快速排序友好。 快速排序数据是顺序访问的,可以做缓存处理; 堆排序数据是跳着访问的,对
CPU缓存不友好。 - 对于相同的数据,在排序过程中,堆排序算法的数据交换次数要多余快速排序。堆排序的第一步是建堆,建堆的过程会打乱数据原有的相对先后顺序,导致源数据的有序度降低。对于一组已经有序的数据来说,经过建堆之后,数据反而变得更加无序了。
# 6、堆的应用
# 1、优先级队列
优先级队列中,数据的出队顺序不是先进先出,而是按照优先级来,优先级最高的,最先出队。 堆和优先级队列非常相似。一个堆就可以看成是一个优先级队列。很多时候,它们只是概念上的区分而已。往优先级队列中插入一个元素,就相当于往堆中插入一个元素;从优先级队列中取出优先级最高的元素,就相当于取出堆顶元素。
# 1、合并有序小文件
我们将从小文件中取出来的字符串放入到小顶堆中,那堆顶的元素,也就是优先级队列队首的元素,就是最小的字符串。我们将这个字符串放入到大文件中,并将其从堆中删除。然后再从小文件中取出下一个字符串,放入到堆中。循环这个过程,就可以将 100 个小文件中的数据依次放入到大文件中。
# 2、高性能定时器
假设我们有一个定时器,定时器中维护了很多定时任务,每个任务都设定了一个要触发执行的时间点。定时器每过一个很小的单位时间(比如 1 秒),就扫描一遍任务,看是否有任务到达设定的执行时间。如果到达了,就拿出来执行。
但是,这样每过 1 秒就扫描一遍任务列表的做法比较低效,主要原因有两点:
- 第一,任务的约定执行时间离当前时间可能还有很久,这样前面很多次扫描其实都是徒劳的;
- 第二,每次都要扫描整个任务列表,如果任务列表很大的话,势必会比较耗时。
我们按照任务设定的执行时间,将这些任务存储在优先级队列中,队列首部(也就是小顶堆的堆顶)存储的是最先执行的任务。它拿队首任务的执行时间点,与当前时间点相减,得到一个时间间隔 T。
这个时间间隔 T 就是,从当前时间开始,需要等待多久,才会有第一个任务需要被执行。这样,定时器就可以设定在 T 秒之后,再来执行任务。从当前时间点到(T-1)秒这段时间里,定时器都不需要做任何事情。当 T 秒时间过去之后,定时器取优先级队列中队首的任务执行。然后再计算新的队首任务的执行时间点与当前时间点的差值,把这个值作为定时器执行下一个任务需要等待的时间。这样,定时器既不用间隔 1 秒就轮询一次,也不用遍历整个任务列表,性能也就提高了。
# 2、利用堆求Top K
var findKthLargest = function(arr, k) {
// return nums.sort((a,b)=>b-a)[k-1];
buildHeap(arr);
let len=arr.length-1;
while(k>1){
//将堆顶元素放到最后排好序的数组的首位
[arr[0],arr[len]]=[arr[len],arr[0]];
len--;
k--;
//将最大元素调整到堆顶
heapify(arr,len,0)
}
return arr[0]
};
function buildHeap (arr) {
const len = arr.length;
//最后一个非叶子节点的索引
let i = Math.floor(len / 2)-1;
for (; i >= 0; i--) {
heapify(arr, len-1, i)
}
}
function heapify (arr, n, i) {
while (true) {
let maxPos = i;
if (i * 2 + 1 <= n && arr[i] < arr[i * 2 + 1]) maxPos = i * 2 + 1;
if (i * 2 + 2 <= n && arr[maxPos] < arr[i * 2 + 2]) maxPos = i * 2 + 2;
if (maxPos == i) break;
//交换位置
[arr[i], arr[maxPos]] = [arr[maxPos], arr[i]]
i = maxPos;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 3、利用堆求中位数
← 数据结构之图 数据结构之字符串总结 →