# 贪心算法
又称 贪婪算法,贪心算法是一种寻找 局部最优解 为手段从而达成整体解决方案的算法。在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
基本要素
- 贪心选择:贪心选择是指所求问题的整体最优解可以通过一系列 局部最优 的选择,即贪心选择来达到。贪心选择是采用从顶向下、以迭代的方法做出相继选择,每做一次贪心选择就将所求问题简化为一个规模更小的子问题。然后,用数学归纳法证明,通过每一步贪心选择,最终可得到问题的一个整体最优解。
- 最优子结构:当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。
基本思路
- 建立数学模型来描述问题;
- 把求解的问题分成若干个子问题;
- 对每一子问题求解,得到问题的局部最优解;
- 把子问题的局部最优解合成原来问题的一个解;
贪心算法解决问题步骤分析
- 第一步,当我们看到这类问题的时候,首先联想到贪心算法: 针对一组数据,我们定义了 限制值和期望值 ,希望从中选出几个数据,在满足限制值的情况下,期望值最大。如背包问题,限制值就是背包的大小,期望值就是物品的最大价值。
- 第二步,我们尝试看下这个问题是否可以用贪心算法解决: 每次选择当前情况下,在对限制值同等贡献量的情况下,对期望值贡献最大 的数据。如背包问题,每次都是选择单价最高的,也就是重量相等的情况下,对价值贡献最大的物品。
- 第三步,举几个例子看下贪心算法产生的结果是否是最优的。 从实践的角度讲,大部分能用贪心算法解决的问题,贪心算法的正确性都是显而易见的,不需要严格的数学推导证明。
动态规划和贪心算法的区别
- 贪心算法的每一次操作都对结果产生直接影响,而动态规划则不是;
- 贪心算法对每个子问题的解决方案都做出选择,不能回退;
- 动态规划则会根据以前的选择结果对当前进行选择,有回退功能;
- 动态规划主要运用于 二维或三维 问题,而贪心一般是 一维 问题。
下面利用贪心算法来解决一些经典问题。
# 1、找零问题
# 题目1
你从商店购买了一些商品,找零 63 美分,店员要怎样给你这些零钱才能得到最少的硬币?
分析
- 在生活中,我们肯定是先用面值大的来支付,如果不够,就继续用更小一点的面值的,以此类推,最后剩下的用1元来补齐。
- 这个问题的限制值 是63美分,期望值 是给出的硬币数最少。
function makeChange (origAmt, coins = {}) {
if (origAmt % 25 < origAmt) {
coins[25] = parseInt(origAmt / 25);
origAmt = origAmt % 25;
}
if (origAmt % 10 < origAmt) {
coins[10] = parseInt(origAmt / 10);
origAmt = origAmt % 10;
}
if (origAmt % 5 < origAmt) {
coins[5] = parseInt(origAmt / 5);
origAmt = origAmt % 5;
}
coins[1] = parseInt(origAmt / 1);
const count = Object.values(coins).reduce((cur, next) => {
return cur + next
})
return count
}
var origAmt = 63;
makeChange(origAmt);
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 2、背包问题
# 题目 1
物品 A B C D
价格 50 220 60 60
重量 5 20 10 12
比率 10 11 6 5
2
3
4
思路
- 背包的容量是
W,物品的价格是v, 重量是w。 - 根据
v/w的比率对物品排序。 - 按比率的降序方式来考虑物品。
- 尽可能多的放入每个物品。
function greedy (values, weights, capacity) {
var returnValue = 0
var remainCapacity = capacity
var sortArray = []
//1、计算每个物品的单位重量的价值
values.map((value, index) => {
sortArray.push({
'value': value,
'weight': weights[index],
'ratio': value / weights[index]
})
})
//2、按单位价值降序排序
sortArray.sort(function (a, b) {
return b.ratio - a.ratio
})
let obj, num;
//3、根据背包当前所剩容量选取物品
while (remainCapacity && (obj = sortArray.shift())) {
num = parseInt(remainCapacity / obj.weight)
remainCapacity -= num * obj.weight
//4、如果背包的容量大于当前物品的重量,那么就将当前物品装进去,否则循环结束
returnValue += num * obj.value
}
return returnValue
}
var items = ['A', 'B', 'C', 'D']
var values = [50, 220, 60, 60]
var weights = [5, 20, 10, 12]
var capacity = 32 //背包容积
greedy(values, weights, capacity) // 320
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 3、区间覆盖
假设我们有 n 个区间,区间的起始端点和结束端点分别是[l1, r1],[l2, r2],[l3, r3],……,[ln, rn]。我们从这 n 个区间中选出一部分区间,这部分区间满足两两不相交(端点相交的情况不算相交),最多能选出多少个区间呢?
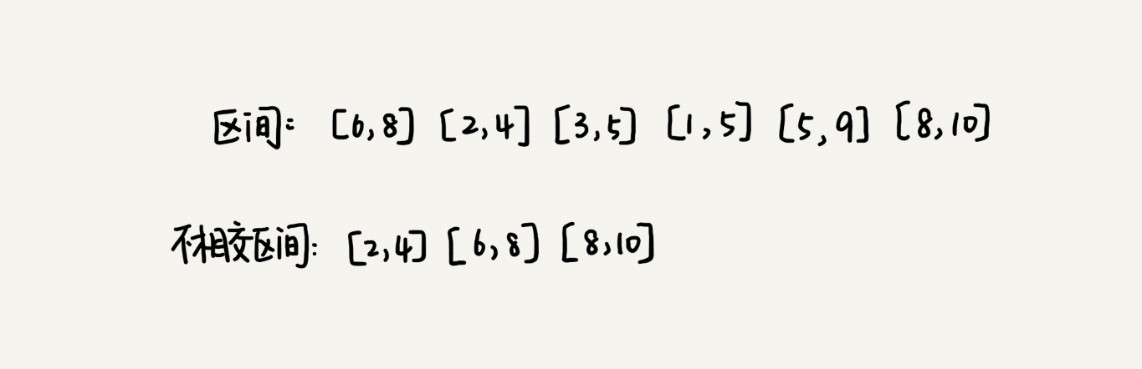
解决思路:
- 假设这 n 个区间中最左端点是
lmin,最右端点是rmax。这个问题就相当于,我们选择几个不相交的区间,从左到右将[lmin, rmax]覆盖上。我们 按照起始端点从小到大的顺序 对这 n 个区间 排序。 - 每次选择的时候,左端点跟前面的已经覆盖的区间不重合的,右端点又尽量小的,这样可以让剩下的未覆盖区间尽可能的大,就可以放置更多的区间。这实际上就是一种贪心的选择方法。
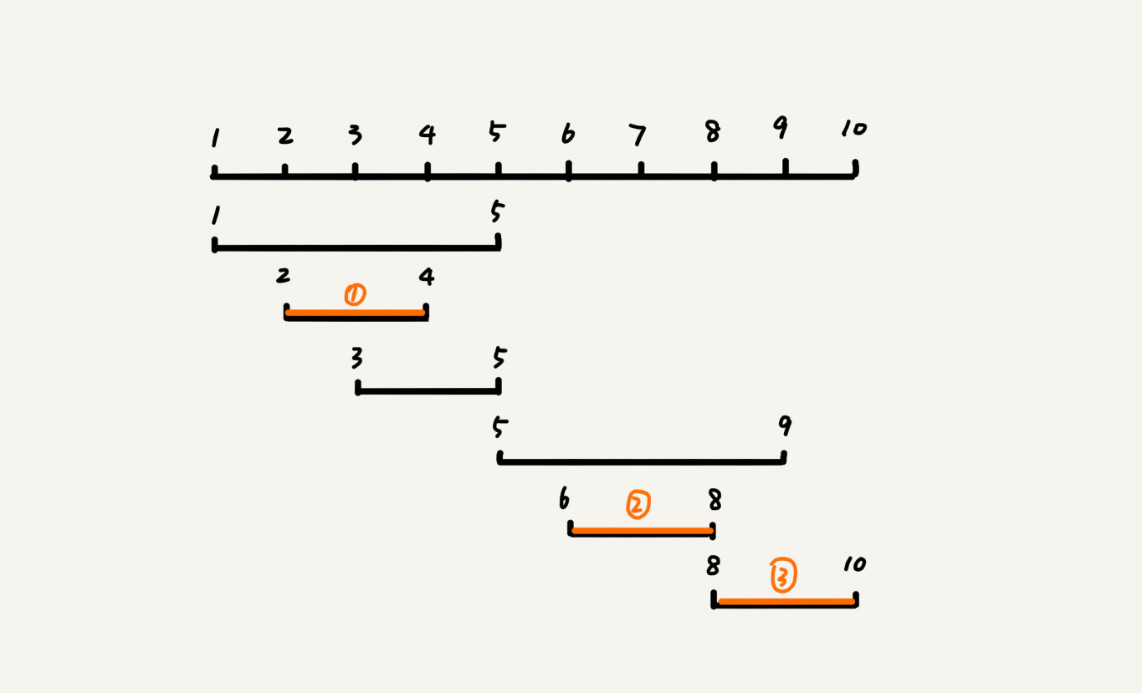
# 题目1、活动安排问题
设有n个活动的集合
E={1,2,…,n},其中每个活动都要求使用同一资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi,且si <fi。要求设计程序,使得安排的活动最多。
问题分析:
设有 n 个活动的集合{0,1,2,…,n-1},其中每个活动都要求使用同一资源,如会场等,而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间 starti 和一个结束时间 endi ,且 starti<endi。如选择了活动i,则它在半开时间区间 [starti,endi) 内占用资源。若区间 [starti,endi) 与区间 [startj,endj) 不相交,称活动i与活动j是相容的。
function getMaxActivitis(start,end,n){
//将开始时间和结束时间构造成一个对象
let obj={}
for(let i=0;i<n;i++){
obj[i]={start:start[i],end:end[i]}
}
//按结束时间升序排列
const keysArr=Object.keys(obj).sort((a,b)=>obj[a].end-obj[b].end)
//用于存放合适时间的活动
const arr=[]
//用于记录合适时间的索引
let index=0;
arr.push([obj[keysArr[0]].start,obj[keysArr[0]].end])
for(let i=1;i<keysArr.length;i++){
if(obj[index].end<=obj[i].start){
index=i;
arr.push([obj[i].start,obj[i].end])
}
continue;
}
return arr.length;
}
const start = [0,1,3,0,5,3,5,6,8,8,2,12];
const end=[0,4,5,6,7,8,9,10,11,12,13,14]
getMaxActivitis(start,end,start.length)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 题目2、任务调度问题
# 题目3、教师排课
# 4、分糖果
# 题目1
我们有
m个糖果和n个孩子。我们现在要把糖果分给这些孩子吃,但是糖果少,孩子多(m<n),所以糖果只能分配给一部分孩子。 每个糖果的大小不等,这 m 个糖果的大小分别是 s1,s2,s3,……,sm。除此之外,每个孩子对糖果大小的需求也是不一样的,只有糖果的大小大于等于孩子的对糖果大小的需求的时候,孩子才得到满足。假设这 n 个孩子对糖果大小的需求分别是 g1,g2,g3,……,gn。求解怎么分糖果,能尽可能满足最多数量的孩子?
分析:
从
n个孩子中,抽取一部分孩子分配糖果,让满足的孩子的个数(期望值)是最大的。这个问题的限制值就是糖果个数m。对于一个孩子来说,如果小的糖果可以满足,我们就没必要用更大的糖果,这样更大的就可以留给其他对糖果大小需求更大的孩子。
另一方面,对糖果大小需求小的孩子更容易被满足,所以,我们可以从需求小的孩子开始分配糖果。因为满足一个需求大的孩子跟满足一个需求小的孩子,对我们期望值的贡献是一样的。
我们每次从剩下的孩子中,找出对糖果大小需求最小的,然后发给他剩下的糖果中能满足他的最小的糖果,这样得到的分配方案,也就是满足的孩子个数最多的方案。
# 5、霍夫曼编码
霍夫曼编码是一种十分有效的编码方法,广泛用于数据压缩中,其压缩率通常在 20%~90% 之间。霍夫曼编码不仅会考察文本中有多少个不同字符,还会考察每个字符出现的频率,根据频率的不同,选择不同长度的编码。
霍夫曼编码试图用这种不等长的编码方法,来进一步增加压缩的效率。如何给不同频率的字符选择不同长度的编码呢?根据贪心的思想,我们可以把 出现频率比较多的字符,用稍微短一些的编码;出现频率比较少的字符,用稍微长一些的编码。
霍夫曼编码是不等长的,每次应该读取 1 位还是 2 位、3 位等等来解压缩呢?这个问题就导致霍夫曼编码解压缩起来比较复杂。为了避免解压缩过程中的歧义,霍夫曼编码要求各个字符的编码之间,不会出现某个编码是另一个编码前缀的情况。
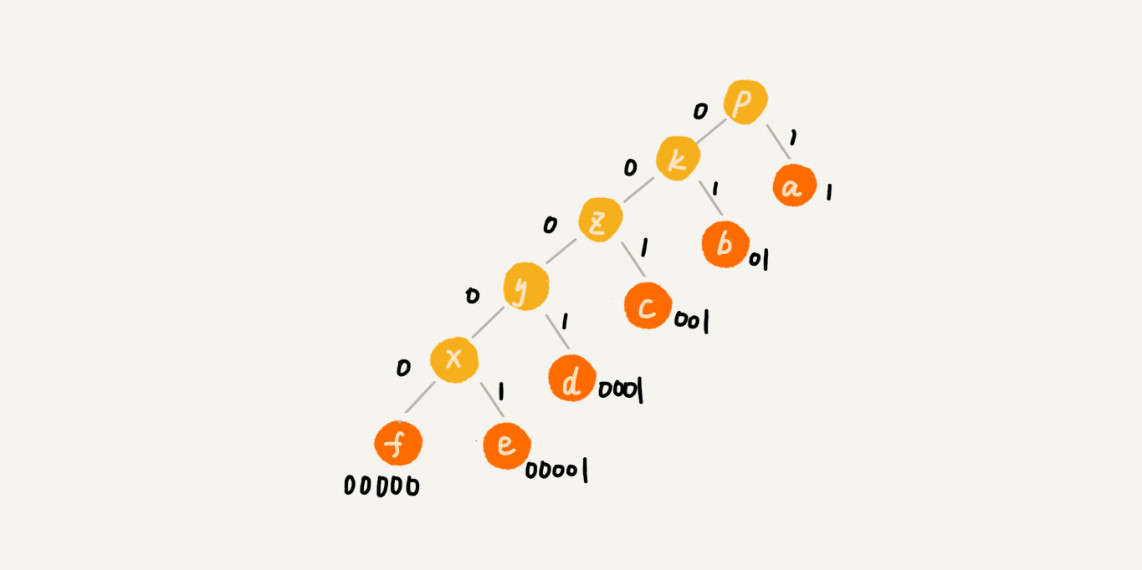
假设 a、b、c、d、e、f这 6 个字符出现的频率从高到低依次是 a、b、c、d、e、f。我们把它们编码下面这个样子,任何一个字符的编码都不是另一个的前缀,在解压缩的时候,我们每次会读取尽可能长的可解压的二进制串,所以在解压缩的时候也不会歧义。
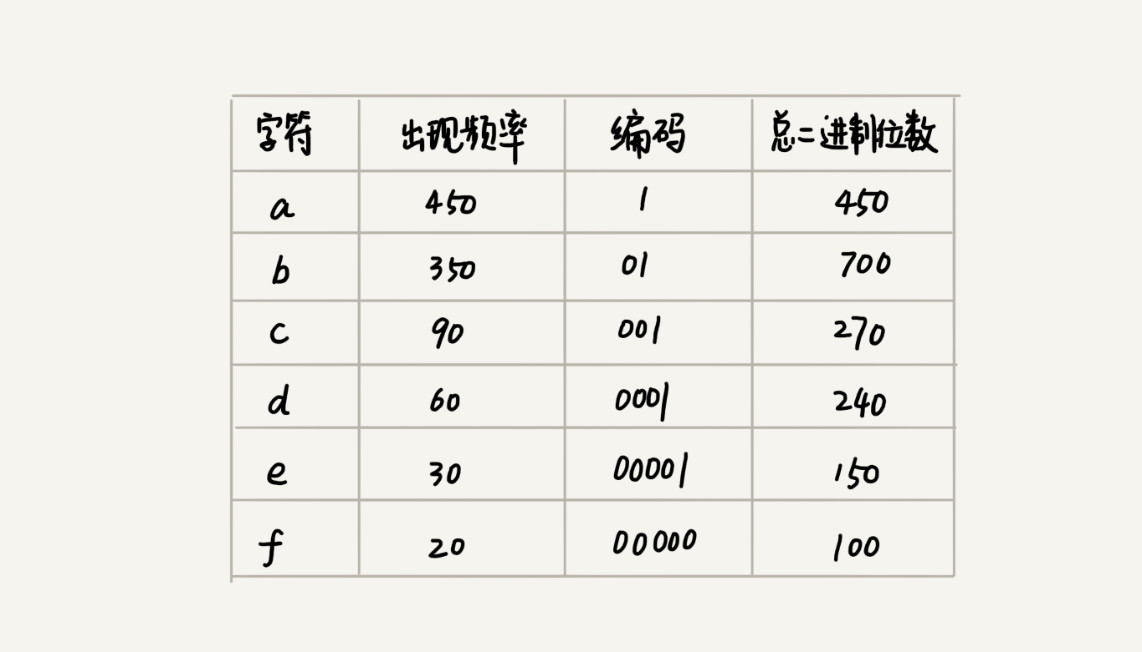
原理分析: 把每个字符看作一个节点,并且附带着把频率放到优先级队列中。我们从队列中取出频率最小的两个节点 A、B,然后新建一个节点 C,把频率设置为两个节点的频率之和,并把这个新节点 C 作为节点 A、B 的父节点。最后再把 C 节点放入到优先级队列中。重复这个过程,直到队列中没有数据。
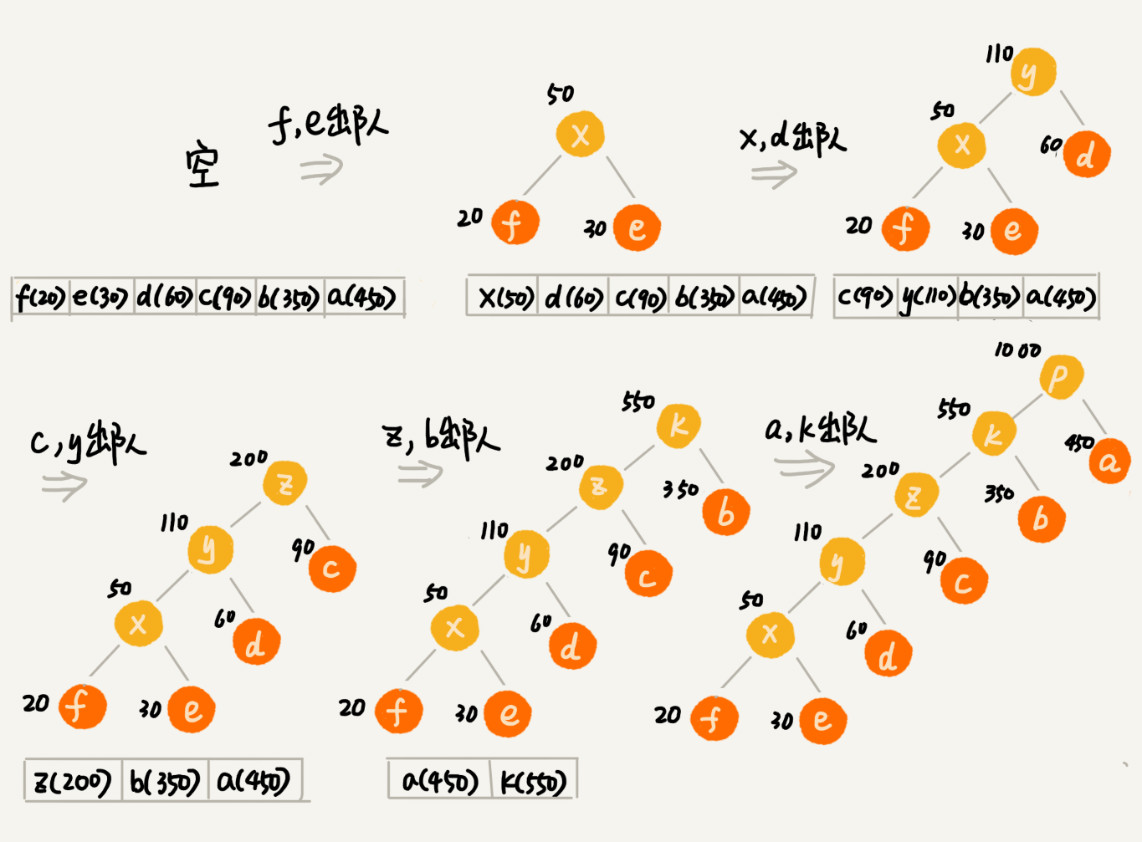
给每一条边加上画一个权值,指向左子节点的边我们统统标记为 0,指向右子节点的边,我们统统标记为 1,那从根节点到叶节点的路径就是叶节点对应字符的霍夫曼编码。
 参考资料
参考资料
← 算法基本思想之回溯算法 广度和深度优先遍历 →