# 1、欧拉角
欧拉角是飞控系统中用于描述飞行器姿态的方式,使用三个角度来表示,分别是yaw偏航角、pitch俯仰角、roll 滚转角。
- yaw:偏航角,是指飞行器偏离原来航线的角度。
- pitch:俯仰角,是指飞行器机头抬起的角度。
- roll:滚转角,是指飞行器绕着自身头尾轴线翻滚的角度。
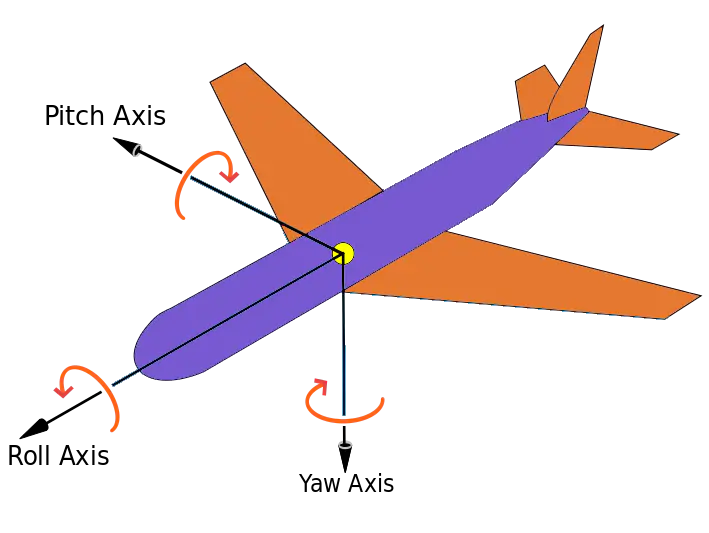
(图片来源于网络)
对比到笛卡尔坐标系,偏航角是绕着 Y 轴旋转的角度 α,俯仰角是绕着 X 轴旋转的角度 β,滚转角是绕着 Z 轴旋转的角度 γ。
注意: 欧拉角旋转时绕的轴系,既可以参照世界坐标系,也可以参照自身坐标系。本文所讲的都是参考自身坐标系。
欧拉角很容易就能表示出一个旋转运动,而且用角度来描述旋转。如 R=(α,β,γ)。
欧拉角旋转顺序有很多种。如XYX,XZX,YZY,YXY,ZXZ,ZYZ。
# 1、欧拉角的矩阵表示
以 XYZ 顺序为例,XYZ 顺序的欧拉旋转可以表示如下:

上面的公式有两种理解方式:
- 参照自身坐标系,先绕
X轴旋转,再绕Y轴旋转,最后绕Z轴旋转。 - 参照世界坐标系,先绕
Z轴旋转,再绕Y轴旋转,最后绕X轴旋转。
根据R=(90,90,90)欧拉角,分别根据自身坐标系旋转和根据世界坐标系来旋转发现,旋转之后的结果是一样的。
从而我们可以得到一个结论:一个复合变换矩阵,既可以理解为世界坐标系下的依次变换,也可以理解为模型坐标系下的依次变换,变换顺序相反。
# 2、根据欧拉角推导旋转矩阵
按照 XYZ 的顺序推导旋转矩阵,如下所示:
根据上面的推导公式,自然不难用javascript来实现一遍了。
function makeRotationFromEuler(euler, target){
target = target || new Float32Array(16);
var x = euler.x, y = euler.y, z = euler.z;
var cx = Math.cos(x), sx = Math.sin(x),
cy = Math.cos(y), sy = Math.sin(y),
cz = Math.cos(z), sz = Math.sin(z);
var sxsz = sx * sz;
var cxcz = cx * cz;
var cxsz = cx * sz;
var sxcz = sx * cz;
target[0] = cy * cz;
target[1] = sxcz * sy + cxsz;
target[2] = sxsz - cxcz * sy;
target[3] = 0;
target[4] = -cy * sz;
target[5] = cxcz - sxsz * sy;
target[6] = sxcz + cxsz * sy
target[7] = 0;
target[8] = sy;
target[9] = -sx * cy;
target[10] = cx * cy;
target[11] = 0;
target[12] = 0;
target[13] = 0;
target[14] = 0;
target[15] = 1;
return target;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 3、欧拉角的缺点
计算过程涉及到大量三角函数计算,运算量大,这点在推导公式的过程中显而易见。
给定方位的欧拉角不唯一,有多个,这会对旋转动画的插值造成困难。同样一个姿态可以由好多个欧拉角来表示,即多对一的关系,那么在插值过程中就可能会引起姿态突变,产生抖动效果。
万向死锁,这个现象会在第二个旋转轴旋转了90 度时产生,当第二个旋转轴旋转 90 度时,会导致第三个旋转轴和第一个旋转轴重合,此时如果继续绕第三个旋转轴,相当于在第一个旋转轴上旋转。所谓死锁并不是旋转不了了,而是少了一个自由度。
由于万向死锁的问题:
1、欧拉角(x: 80, y: 90, z: 0)和(x: 30, y: 90, z: 50) 表示的旋转一模一样。多个欧拉角会对应一个旋转。这在做旋转动画时会导致旋转动画不准确的问题。
2、欧拉角(x: 47, y: 90, z:55)和(x: 8, y: 0, z: 0)和(x: 55, y: 90, z:55),这两个欧拉角最终的旋转效果也是不一样的。
结论:实际上欧拉角足以应对大部分场景,虽然它有一些缺点。我们可以做出一些限制来避免它们,比如我们可以将第二个旋转轴的旋转角度限制在 -90 到 +90 之间。但尽管如此,我们仍然无法规避死锁的产生。
# 2、四元数
# 1、四元数的定义
四元数,是一种超复数,由4个实数加上3个虚数单位(i,j,k)组成,可以表示为:q = (w, x, y, z)或者q = w + xi + yj + zk。并且有以下特点。
$$
{i^2}= j^2 = k^2 = ijk = -1
且ij=k、jk=i、ki=j
$$
四元数还可以以向量的形式表示
$$
q = (w, u), 其中u = (x, y, z)
$$
# 2、四元素的基本性质
- 共轭:将虚部的系数取反。给定四元数
q=(w,v), 其共轭 $q^$ 为 $q^$ =(w,−v)。 - 模:四元数
q的模|q|为: $$ |q|=\sqrt{w^2+x^2+y^2+z^2} $$ - 单位四元数:模为1的四元数,即
|q| = 1,表示没有缩放的纯旋转。 - 归一化:将四元素
q除以它的模|q|,就可以得到单位四元数: $$ q_{norm} = \frac{q}{|q|} $$
# 3、四元素的运算
- 加法:四元数的加法是逐元素相加: $$ q1+q2 = (w1+w2, x1+x2, y1+y2, z1+z2) $$
- 乘法:四元数的乘法并不是逐元素相乘,而是遵循特定的规则:
其中
⋅表示点积,×表示叉积。 $$ q1q2 = (w1w2-v1 \cdot v2, w1v2+w2v1+v1 × v2) $$ - 旋转:给定一个单位四元数,
q=(cos(θ/2),u*sin(θ/2),其中θ是旋转角度。u是旋转轴的单位向量,旋转一个向量v,可以表示为: $$ v' = qvq^* $$ - 插值:给定两个四元数
q1, q2,以及一个参数t,那么在0≤t≤1之间,可以计算出t对应的四元数: $$ slerp(q1, q2, t) = \frac{sin((1-t)θ)}{sinθ}q1 + \frac{sin(tθ)}{sinθ} $$
# 4、四元数的应用
旋转向量:使用四元数来旋转三维向量,避免万向锁问题。
组合旋转:通过四元数乘法组合多个旋转,保持稳定和高效。
插值动画:在关键帧动画中使用Slerp来平滑地插值旋转,避免突然的旋转变化。
物理模拟:在物理引擎中用四元数表示刚体的旋转,保持精度和稳定性。
# 3、四元数实践
下面是使用 JavaScript 和 glMatrix (opens new window) 库进行四元数操作的示例:
// 引入glMatrix库
import { quat, vec3 } from 'gl-matrix';
// 创建一个单位四元数
let q = quat.create(); // 默认是单位四元数 [0, 0, 0, 1]
// 定义一个旋转:45度绕Z轴旋转
let angle = Math.PI / 4; // 45度
let axis = vec3.fromValues(0, 0, 1);
quat.setAxisAngle(q, axis, angle); // 设置旋转
// 使用四元数旋转一个向量
let v = vec3.fromValues(1, 0, 0);
let v_rotated = vec3.create();
vec3.transformQuat(v_rotated, v, q);
console.log('Rotated vector:', v_rotated); // 输出旋转后的向量
// 组合旋转
let q1 = quat.create();
let q2 = quat.create();
quat.setAxisAngle(q1, [0, 1, 0], Math.PI / 2); // 90度绕Y轴旋转
quat.setAxisAngle(q2, [1, 0, 0], Math.PI / 2); // 90度绕X轴旋转
let q_combined = quat.create();
quat.multiply(q_combined, q1, q2); // 组合旋转
// 插值两个四元数
let t = 0.5; // 插值因子
let q_slerp = quat.create();
quat.slerp(q_slerp, q1, q2, t);
console.log('Slerp result:', q_slerp);
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
