# 1.光源类型
真实世界中的光主要有2种类型,平行光和点光源光:类似于电灯泡发出的光。 同时我们还会用环境光来模拟真实世界中的非直射光(也就是由光源发出后经过墙壁或者其他物体反射后的光)。三维图形学中会使用一些其他类型的光,比如聚光等光。
# 1.平行光
光线平行,具有方向。可以用一个方向和颜色来定义。
# 2.点光源光
点光源光是从一个点向周围的所有方向发出的光。定义点光源时我们需要指定点光源的位置和颜色。
# 3.环境光
指那些经光源发出后,被墙壁等物体多次反射,然后照到物体表面上的光。环境光从各个角度照射物体,起强度都是一致的。环境光不用指定位置和方向,只需要指定颜色就行。
# 2.反射类型
根据物体表面反射光线的方式,可以分为漫反射和环境反射。
# 1.漫反射
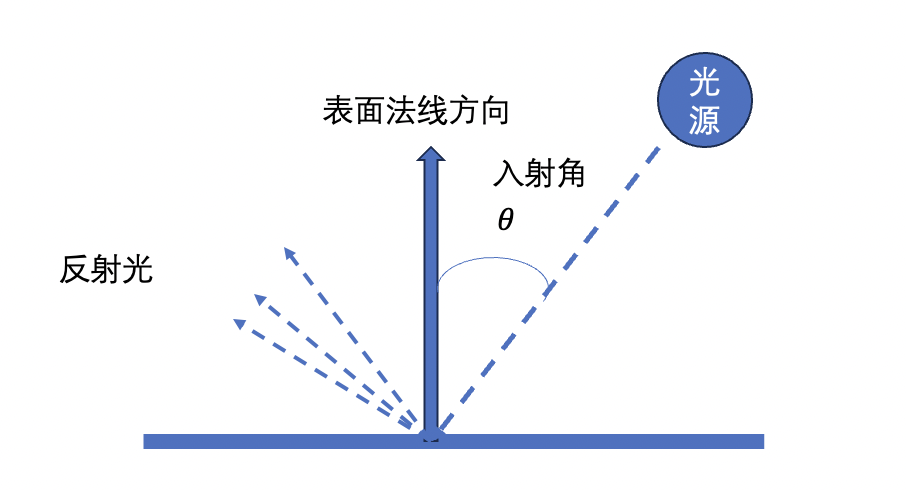
漫反射是针对平行光和点光源而言的,漫反射的反射光在各个方向上都是均匀的。有些物体的表面是粗糙的,在这种情况下,反射光就会以不固定的角度反射出去。
反射光的颜色取决于入射光的颜色、表面的基底色、入射光与表面法线形成的入射角。入射角为入射光与表面的法线形成的夹角,用𝜃 表示 ,漫反射光的颜色可以根据下面的公式计算得到。
漫反射光的颜色计算
物体漫反射光颜色 = 入射光颜色 X 表面基底色 X cos𝜃
# 2.环境反射
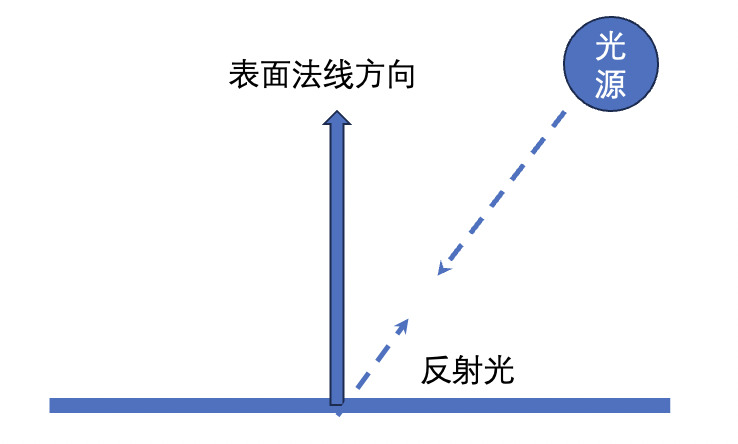
环境反射是针对环境光而言的。 反射光的方向可以认为就是入射光的反方向。由于环境光照射物体的方式就是各方向均匀、强度相等的,所以反射光也是各向均匀的。
- 环境反射光的颜色计算。
物体环境反射光颜色 = 入射光颜色 X 表面基颜色
- 漫反射和环境反射 同时存在时物体的颜色计算
当漫反射和环境反射同时存在时,将两者加起来,就会得到物体最终被观察到的颜色。
物体表面的颜色 = 漫反射光颜色 + 环境反射光颜色
# 3.平行光下的漫反射
上面的cos𝜃可以用两个矢量的点积来得到。下面的等式成立的条件是光线方向和法线方向向量必须都是单位向量。
cos𝜃 = 光线方向 * 法线方向 = |光线方向|*|法线方向|*cos𝜃
所以上面上面的漫反射光的公式可以写成
物体漫反射光颜色 = 入射光颜色 X 表面基底色 X (光线方向 * 法线方向)
注意:
- 光线方向矢量和表面法线矢量的长度必须时
1,否则反射光的颜色就会过暗或者过亮。将一个矢量的长度调整为1,同时保持方向不变的过程称之为归一化。 - 光线方向,实际上是入射方向的反方向,是从入射点指向光源的方向。
法线: 垂直于物体表面的方向,称之为法线或者法向量。因为每个表面都有两个面,所以每个表面都具有两个法向量。
平行光下的漫反射的 顶点着色器中的代码如下所示:
attribute vec4 a_Position;
attribute vec4 a_Color;
attribute vec4 a_Normal; // Normal 法向量
uniform mat4 u_MvpMatrix;
uniform vec3 u_LightColor; // Light color 光线颜色
uniform vec3 u_LightDirection; // Light direction (in the world coordinate, normalized) 光线方向
varying vec4 v_Color;
void main() {
gl_Position = u_MvpMatrix * a_Position ;
// Make the length of the normal 1.0
// 法向量归一化
vec3 normal = normalize(a_Normal.xyz);
// Dot product of the light direction and the orientation of a surface (the normal)
// 计算点积
// 当角度大于90时,将点积赋值为0,表示光线是找到了背面,所以我们看到的物体是暗的。
float nDotL = max(dot(u_LightDirection, normal), 0.0);
// Calculate the color due to diffuse reflection
// 计算漫反射光的颜色
vec3 diffuse = u_LightColor * a_Color.rgb * nDotL;
v_Color = vec4(diffuse, a_Color.a);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
平行光下的漫反射的 主要js代码如下所示
...
const u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
const u_LightColor = gl.getUniformLocation(gl.program, 'u_LightColor');
comst u_LightDirection = gl.getUniformLocation(gl.program, 'u_LightDirection');
if (!u_MvpMatrix || !u_LightColor || !u_LightDirection) {
console.log('Failed to get the storage location');
return;
}
// Set the light color (white)
gl.uniform3f(u_LightColor, 1.0, 1.0, 1.0);
// Set the light direction (in the world coordinate)
var lightDirection = new Vector3([0.5, 3.0, 4.0]);
lightDirection.normalize(); // Normalize
gl.uniform3fv(u_LightDirection, lightDirection.elements);
// Calculate the view projection matrix
var mvpMatrix = new Matrix4(); // Model view projection matrix
mvpMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);
mvpMatrix.lookAt(3, 3, 7, 0, 0, 0, 0, 1, 0);
// Pass the model view projection matrix to the variable u_MvpMatrix
gl.uniformMatrix4fv(u_MvpMatrix, false, mvpMatrix.elements);
...
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
具体的 demo地址 平行光的漫反射 (opens new window) 。
最终的绘制效果如下所示:
从上面的图片中我们可以看到右侧表面是全黑的。这是因为我们没有考虑到环境光对物体的照射效果。所以我们还需要加上物体表面的环境反射光的颜色,才能得到物体表面最终的颜色。
所以我们需要对上面的代码做以下修改。
顶点着色器代码
...
uniform vec3 u_AmbientLight; // Color of an ambient light 环境光
varying vec4 v_Color;
...
void main() {
...
// 计算环境光产生的反射光颜色
vec3 ambient = u_AmbientLight * a_Color.rgb;
v_Color = vec4(diffuse+ambient, a_Color.a);
}
2
3
4
5
6
7
8
9
10
js中也需要添加环境光的代码。
...
const u_AmbientLight = gl.getUniformLocation(gl.program, 'u_AmbientLight');
// Set the ambient light
gl.uniform3f(u_AmbientLight, 0.2, 0.2, 0.2);
...
2
3
4
5
最终的绘制结果如下所示

demo 地址 环境光下的漫反射 (opens new window)
# 3.运动物体的光照效果
物体旋转时,每个表面的法向量都会随之改变。所以我们需要在运动的过程中,需要不断计算更新后的法向量。这里我们会用到逆转置矩阵,将变换之前的法向量乘以模型矩阵的逆转置矩阵就可以得到变换后的法向量。转置逆矩阵就是逆矩阵的转置。
逆矩阵:如果矩阵M的逆矩阵是 R,那么M*R或者R*M的结果都是单位矩阵。
转置:将矩阵的行列进行调换(看上去就像是沿着左上-右下对角线进行了翻转)。
所以求逆转置矩阵主要由以下两个步骤:
- 求原矩阵的逆矩阵
- 将上一步得到的逆矩阵进行转置。 所以我们需要将上一步使用环境光的顶点着色器中的代码再进行以下修改。
...
uniform mat4 u_NormalMatrix
uniform vec3 u_AmbientLight; // Color of an ambient light 环境光
varying vec4 v_Color;
...
void main() {
...
// 计算旋转后的反射光
vec3 normal = normalize(vec3(u_NormalMatrix * a_Normal))
...
// 计算环境光产生的反射光颜色
vec3 ambient = u_AmbientLight * a_Color.rgb;
v_Color = vec4(diffuse+ambient, a_Color.a);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
js中的代码需要做如下修改
// Calculate the matrix to transform the normal based on the model matrix
normalMatrix.setInverseOf(modelMatrix);
normalMatrix.transpose();
// Pass the transformation matrix for normals to u_NormalMatrix
gl.uniformMatrix4fv(u_NormalMatrix, false, normalMatrix.elements);
2
3
4
5
具体demo地址 运动物体的颜色 (opens new window)
# 4.点光源光的着色效果
在对点光源下的物体进行着色时,需要在每个入射点计算点光源在该处的方向。点光源光的方向不是恒定不变的,需要根据每个顶点的位置逐一计算。
顶点着色器中的代码跟上面平行光的代码有点不一样,在这里需要不断在世界坐标系中计算顶点坐标光的方向。
...
uniform mat4 u_ModelMatrix;
...
uniform vec3 u_LightPosition;// 在世界坐标系下光源的位置
...
// 计算顶点的世界坐标
vec4 vertexPosition = u_ModelMatrix * a_Position;
// 计算光线方向并归一化
vec3 lightDirection = normalize(u_LightPosition - vec3(vertexPosition));
2
3
4
5
6
7
8
9
最终的展示效果如下所示:

具体的demo地址 点光源光 (opens new window)
仔细观察会发现立方体表面会有不自然的线条。
这是因为在WebGL系统中会根据顶点的颜色,内插出表面上每个片元的颜色。
但是实际上,点光源照射到一个表面上,所产生的效果(每个片元获得的颜色)与简单使用4个顶点颜色(也是有点光源产生)内插出的效果并不完全相同,所以为了效果更逼真,我们需要对表面的每一点计算光照效果。
下面是逐片元计算模型颜色的例子。
顶点着色器中的代码
attribute vec4 a_Position;
attribute vec4 a_Color;
attribute vec4 a_Normal;
uniform mat4 u_MvpMatrix;
uniform mat4 u_ModelMatrix; // Model matrix
uniform mat4 u_NormalMatrix; // Transformation matrix of the normal
varying vec4 v_Color;
varying vec3 v_Normal;
varying vec3 v_Position;
void main() {
gl_Position = u_MvpMatrix * a_Position;
// Calculate the vertex position in the world coordinate
v_Position = vec3(u_ModelMatrix * a_Position);
v_Normal = normalize(vec3(u_NormalMatrix * a_Normal));
v_Color = a_Color;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
片元着色器中的代码
precision mediump float;
uniform vec3 u_LightColor; // Light color
uniform vec3 u_LightPosition; // Position of the light source
uniform vec3 u_AmbientLight; // Ambient light color
varying vec3 v_Normal;
varying vec3 v_Position;
varying vec4 v_Color;
void main() {
// Normalize the normal because it is interpolated and not 1.0 in length any more
vec3 normal = normalize(v_Normal);
// Calculate the light direction and make its length 1.
vec3 lightDirection = normalize(u_LightPosition - v_Position);
// The dot product of the light direction and the orientation of a surface (the normal)
float nDotL = max(dot(lightDirection, normal), 0.0);
// Calculate the final color from diffuse reflection and ambient reflection
vec3 diffuse = u_LightColor * v_Color.rgb * nDotL;
vec3 ambient = u_AmbientLight * v_Color.rgb;
gl_FragColor = vec4(diffuse + ambient, v_Color.a);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
具体demo地址点光源逐片元光照效果 (opens new window)
# 5.三维点光源-高光效果
观察现实世界中的物体,如果物体表面恰好将光线反射到你眼前, 就会显得非常明亮,像镜子一样。我们可以通过计算光线是否反射到眼前来模拟这种情况。
测试方法:如果入射角和反射角恰好与眼睛和和光源的夹角相同,那么光线就会反射到眼前。

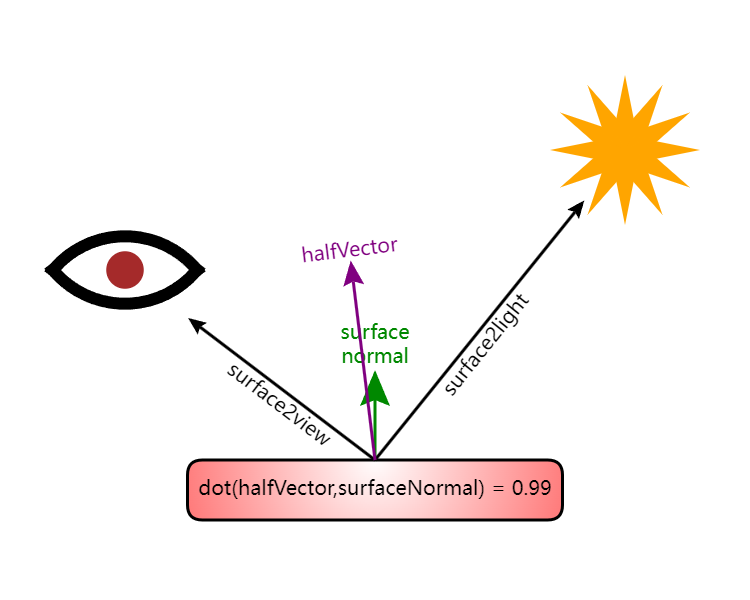
计算方法:根据物体表面到光源的方向,加上物体表面到视点/眼睛/相机的方向,再除以 2 得到 halfVector 向量, 将这个向量和法向量比较,如果方向一致,那么光线就会被反射到眼前。
在着色器中中的代码表示如下所示:
- 顶点着色器
在点元着色器中计算 计算表面到光源的方向 和 计算表面到相机的方向,并将之传入到片元着色器。
attribute vec4 a_position;
attribute vec3 a_normal;
uniform vec3 u_lightWorldPosition;
uniform vec3 u_viewWorldPosition;
uniform mat4 u_world;
uniform mat4 u_worldViewProjection;
uniform mat4 u_worldInverseTranspose;
varying vec3 v_normal;
varying vec3 v_surfaceToLight;
varying vec3 v_surfaceToView;
void main() {
// 将位置和矩阵相乘
gl_Position = u_worldViewProjection * a_position;
// 重定向法向量并传递到片段着色器
v_normal = mat3(u_worldInverseTranspose) * a_normal;
// 计算表面的世界坐标
vec3 surfaceWorldPosition = (u_world * a_position).xyz;
// 计算表面到光源的方向
// 然后传递到片段着色器
v_surfaceToLight = u_lightWorldPosition - surfaceWorldPosition;
// 计算表面到相机的方向
// 然后传递到片段着色器
v_surfaceToView = u_viewWorldPosition - surfaceWorldPosition;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
- 片元着色器
在片元着色器中计算表面到光源和相机之间的 halfVector, 将它和法向量相乘,查看光线是否直接反射到眼前
// 从顶点着色器中传入的值
varying vec3 v_normal;
varying vec3 v_surfaceToLight;
varying vec3 v_surfaceToView;
uniform vec4 u_color;
void main() {
// 由于 v_normal 是可变量,所以经过插值后不再是单位向量,
// 单位化后会成为单位向量
vec3 normal = normalize(v_normal);
vec3 surfaceToLightDirection = normalize(v_surfaceToLight);
vec3 surfaceToViewDirection = normalize(v_surfaceToView);
vec3 halfVector = normalize(surfaceToLightDirection + surfaceToViewDirection);
float light = dot(normal, surfaceToLightDirection);
float specular = dot(normal, halfVector);
gl_FragColor = u_color;
// 只将颜色部分(不包含 alpha) 和光照相乘
gl_FragColor.rgb *= light;
// 直接加上高光
gl_FragColor.rgb += specular;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
在js代码中,我们只需要设置u_lightWorldPosition和u_viewWorldPosition即可
const lightWorldPositionLocation =
gl.getUniformLocation(program, "u_lightWorldPosition");
const viewWorldPositionLocation =
gl.getUniformLocation(program, "u_viewWorldPosition");
...
// 计算相机矩阵
const camera = [100, 150, 200];
const target = [0, 35, 0];
const up = [0, 1, 0];
const cameraMatrix = makeLookAt(camera, target, up);
//设置光源位置
gl.uniform3fv(lightWorldPositionLocation, [20, 30, 60]);
// 设置相机位置
gl.uniform3fv(viewWorldPositionLocation, camera);
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
但是上面计算得到的高光效果并不是我们想要的,太亮了。

为了解决太亮的问题,我们可以将点乘结果(dot(normal, halfVector))进行求幂运算来解决太亮的问题, 它会把高光从线性变换变成指数变换。
specular = pow(dot(normal, halfVector), u_shininess);
为了避免specular = pow(dot(normal, halfVector), u_shininess)得到的结果是赋值,所以我们只将点乘结果(法线方向和表面到光线的方向的点乘)为正(dot(normal, surfaceToLightDirection)>0.0)的部分进行计算,其他部分设置为 0.0。
uniform vec4 u_color;
uniform float u_shininess;
...
void mian(){
float light = dot(normal, surfaceToLightDirection);
float specular = 0.0;
if (light > 0.0) {
specular = pow(dot(normal, halfVector), u_shininess);
}
}
2
3
4
5
6
7
8
9
10
在js中设置u_shininess的值,用于调节亮度。
const shininessLocation = gl.getUniformLocation(program, "u_shininess");
...
// 设置亮度
gl.uniform1f(shininessLocation, shininess);
2
3
4
5
6
如果你还想设置光照颜色和高光颜色的化可以进行如下设置
uniform vec4 u_color;
uniform float u_shininess;
uniform vec3 u_lightColor;
uniform vec3 u_specularColor;
...
void main() {
// 只将颜色部分(不包含 alpha) 和光照相乘
gl_FragColor.rgb *= light * u_lightColor;
// 直接和高光相加
gl_FragColor.rgb += specular * u_specularColor;
}
2
3
4
5
6
7
8
9
10
11
12
13
在js中设置u_lightColor和u_specularColor的值
const lightColorLocation =
gl.getUniformLocation(program, "u_lightColor");
const specularColorLocation =
gl.getUniformLocation(program, "u_specularColor");
...
// 设置光照颜色
gl.uniform3fv(lightColorLocation, m4.normalize([1, 0.6, 0.6])); // 绿光
// 设置高光颜色
gl.uniform3fv(specularColorLocation, m4.normalize([1, 0.6, 0.6])); // 红光
2
3
4
5
6
7
8
9
下面是视觉效果

demo地址 镜面高光效果 (opens new window)
# 6.聚光灯的着色效果
# 1.聚光灯的原理
把点光源想象成一个点,光线从那个点照向所有方向。 实现聚光灯只需要以那个点为起点选择一个方向,作为聚光灯的方向, 然后将其他光线方向与所选方向点乘,然后随意选择一个限定范围, 然后判断光线是否在限定范围内,如果不在就不照亮。
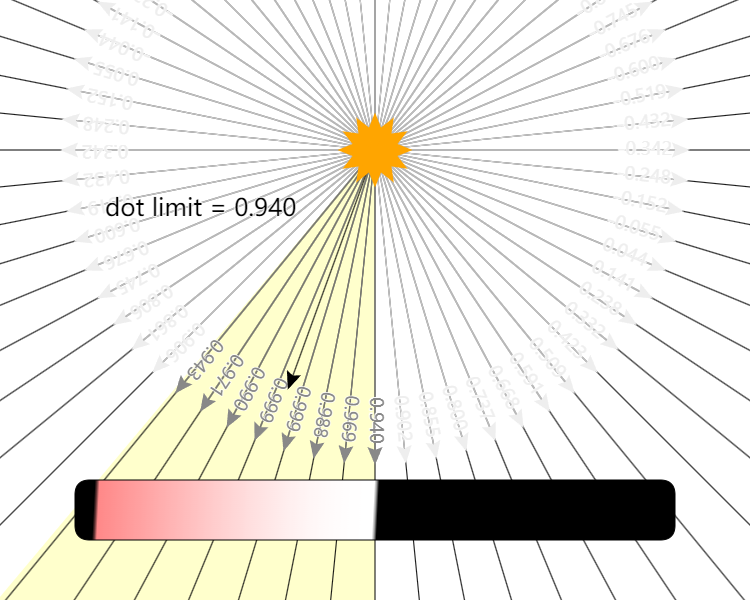
在上方的图示中我们可以看到光线照向所有的方向,并且将每个方向的点乘结果显示在上面。 然后指定一个方向表示聚光灯的方向,选择一个限定(上方以度为单位)。计算dot(surfaceToLight, -lightDirection)的点乘结果。如果点乘结果大于这个限定,就照亮,否则不照亮。计算公式如下:
dotFromDirection = dot(surfaceToLight, -lightDirection)
if (dotFromDirection >= limitInDotSpace) {
// 使用光照
}
2
3
4
# 2.代码实现
计算聚光灯效果的代码我们只需要在上面计算高光效果上的片元着色器代码做出如下修改就行。
// 从顶点着色器传入的值
varying vec3 v_normal;
varying vec3 v_surfaceToLight;
varying vec3 v_surfaceToView;
uniform vec4 u_color;
uniform float u_shininess;
uniform vec3 u_lightDirection;// 聚光灯的方向
uniform float u_limit; // 在点乘空间中
void main() {
// 因为 v_normal 是可变量,被插值过
// 所以不是单位向量,单位可以让它成为再次成为单位向量
vec3 normal = normalize(v_normal);
vec3 surfaceToLightDirection = normalize(v_surfaceToLight);
vec3 surfaceToViewDirection = normalize(v_surfaceToView);
vec3 halfVector = normalize(surfaceToLightDirection + surfaceToViewDirection);
float light = 0.0;
float specular = 0.0;
float dotFromDirection = dot(surfaceToLightDirection,
-u_lightDirection);
if (dotFromDirection >= u_limit) {
light = dot(normal, surfaceToLightDirection);
if (light > 0.0) {
specular = pow(dot(normal, halfVector), u_shininess);
}
}
// 如果光线在聚光灯范围内 inLight 就为 1,否则为 0。 跟上面计算specular等价
//float inLight = step(u_limit, dotFromDirection);
//float light = inLight * dot(normal, surfaceToLightDirection);
//float specular = inLight * pow(dot(normal, halfVector), u_shininess);
gl_FragColor = u_color;
// 只将颜色部分(不包含 alpha) 和光照相乘
gl_FragColor.rgb *= light;
// 直接加上高光
gl_FragColor.rgb += specular;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
在js中设置聚光灯的方向和限定
const lightDirection = [0, 0, 1];
const limit = degToRad(20);
...
const lightDirectionLocation = gl.getUniformLocation(program, "u_lightDirection");
const limitLocation = gl.getUniformLocation(program, "u_limit");
...
const lmat = m4.lookAt(lightPosition, target, up);
lmat = m4.multiply(m4.xRotation(lightRotationX), lmat);
lmat = m4.multiply(m4.yRotation(lightRotationY), lmat);
// get the zAxis from the matrix
// negate it because lookAt looks down the -Z axis
lightDirection = [-lmat[8], -lmat[9],-lmat[10]];
gl.uniform3fv(lightDirectionLocation, lightDirection);
gl.uniform1f(limitLocation, Math.cos(limit));
2
3
4
5
6
7
8
9
10
11
12
13
14
15
注意:
gl.uniform1f(limitLocation, Math.cos(limit));这里设置的是点乘空间中的限定,而不是角度。lightDirection光照方向随着模型的旋转也要改变,所以需要重新计算。
此时得到的光照效果如下,非常粗糙和僵硬。只有在聚光灯范围内才有光照效果, 在外面就直接变黑,没有任何过渡。

# 3.平滑过渡
为了解决上面的问题,我们需要对光照进行平滑过渡。我们可以使用两个限定值代替原来的一个, 一个内部限定一个外部限定。如果在内部限定内就使用 1.0, 在外部限定外面就使用 0.0,在内部和外部限定之间就使用 1.0 到 0.0 之间的插值。
uniform float u_innerLimit; // 在点乘空间中
uniform float u_outerLimit; // 在点乘空间中
...
void main() {
float dotFromDirection = dot(surfaceToLightDirection,
-u_lightDirection);
float limitRange = u_innerLimit - u_outerLimit;
// 计算插值,将之前接近1的值变成0~1之间的值
float inLight = clamp((dotFromDirection - u_outerLimit) / limitRange, 0.0, 1.0);
float light = inLight * dot(normal, surfaceToLightDirection);
float specular = inLight * pow(dot(normal, halfVector), u_shininess);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
上面的代码中我们使用了clamp函数,它可以将值限制在指定范围内。我们可以使用smoothstep对上面的inLight的求取进行以下简化。
float dotFromDirection = dot(surfaceToLightDirection,
-u_lightDirection);
float inLight = smoothstep(u_outerLimit, u_innerLimit, dotFromDirection);
float light = inLight * dot(normal, surfaceToLightDirection);
float specular = inLight * pow(dot(normal, halfVector), u_shininess);
2
3
4
5
smoothstep 和 step 相似返回一个 0 到 1 之间的值,但是它获取最大和最小边界值,返回该值在边界范围映射到 0 到 1 之间的插值。
smoothstep(lowerBound, upperBound, value)
最终的聚光灯效果如下所示

完整demo地址 聚光灯 (opens new window)
参考文档
WebGL 三维点光源 (opens new window)
WebGL 三维方向光源 (opens new window)
WebGL 三维聚光灯 (opens new window)
评 论: