# 1.三维透视投影的定义
透视投影的最终目的是将三维点投影到二维平面上,并通过 透视除法(透视校正) 来模拟人眼的视觉效果。我们通过构建一个透视投影矩阵,将三维坐标系中的点变换到裁剪坐标系,然后通过透视除法得到标准化设备坐标(NDC)。
正射投影看到的物体都是按照近大远小的规则来呈现的。与模型跟观察者的距离有直接的关系。 这种近大远小的效果就赋予了模型深度感,或者称之为透视感。
透视投影,可视范围是一个棱锥体盒子,下面是透视投影的可视范围的示意图。 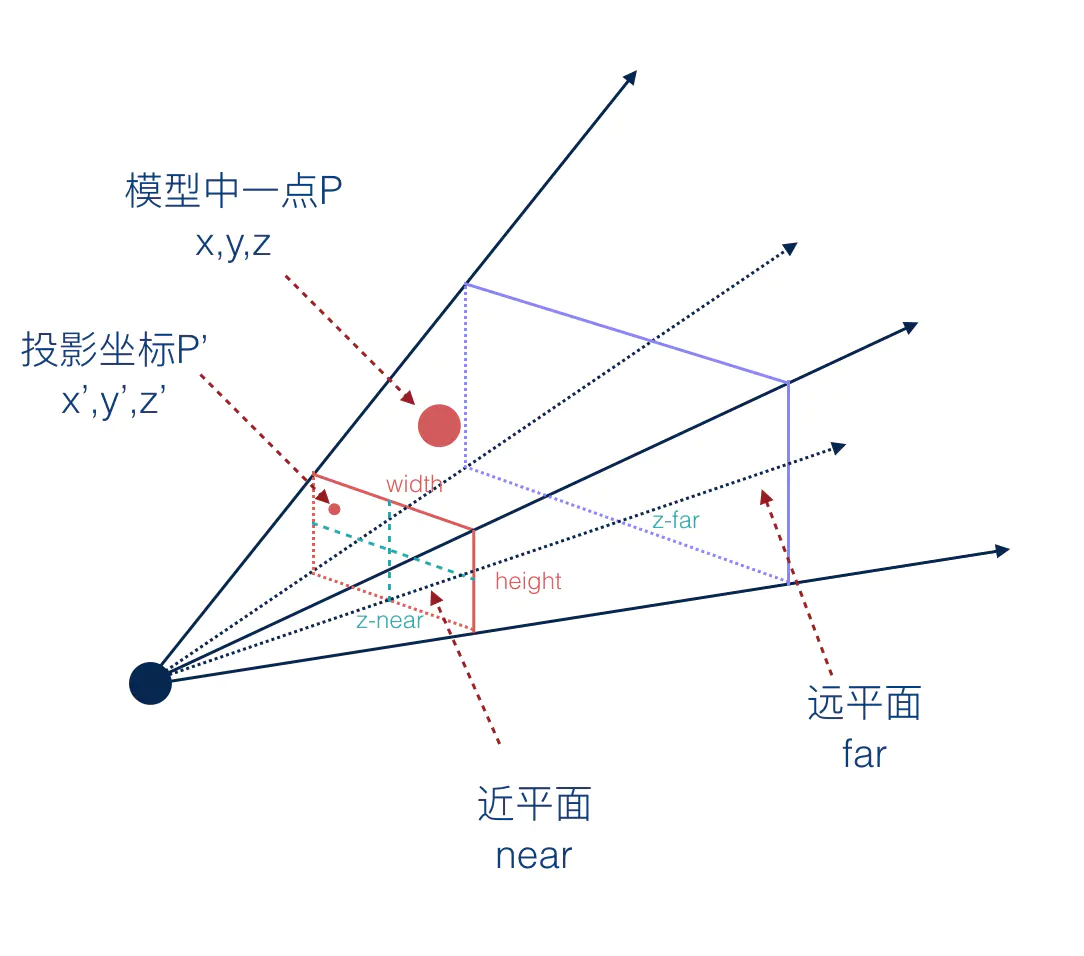
# 2.视锥体的定义
透视投影,可视范围是一个视锥体,定义视锥体时会用到以下参数:
- 视角
(Field of View, FOV):垂直视角的角度。 - 宽高比
(AspectRatio):视口的宽高比width/height。 - 近平面
(Near Plane, n:距离相机最近的平面z-near。 - 远平面
(Far Plane, f:距离相机最远的平面z-far。
# 3推导步骤
# 3.1定义视角参数
视角参数包括视角 (FOV)、宽高比(aspectRatio)、近平面n和远平面f。
θ为视角的一半,即θ = FOV/2t = n * tan(θ)为近平面的高度的一半height/2r = t*aspectRatio = n * tan(θ) * aspectRatio为近平面的宽度的一半wight/2
# 3.2 透视投影矩阵的推导
透视投影矩阵的推导包括将三维点映射到二维平面上,并进行透视除法以实现透视效果。
接下来我们将推导一下透视投影的矩阵是如何得到的。
假设模型中有一个点p(x,y,z)表示像素坐标,投影到近平面后的坐标为p'(x',y',z'),表示投影坐标。
首先我们需要找出 p和 p'之间的关系。p和p'之间的关系可以用如下矩阵来表示。

上面的矩阵运算后可以得到下面的计算结果。
x' = ax + by + cz + d
y' = ex + fy + gz + h
z' = ix + jy + kz + l
w' = mx + ny + oz + p
2
3
4
根据上面的透视投影的示意图,我们根据相似三角形原理,可以得到如下公式。
# 1. x轴
假设一个点在相机坐标系中的位置为(x,y,z),它在近平面上的投影点为 ($x_{proj}$ ,$x_{proj}$,n) 。
根据相似三角形可以得到下面的计算公式。
$$ \frac{x_{proj}}{x} = \frac{n}{z} \Rightarrow x_{proj} = \frac{n}{z} x $$
然后将 $x_{proj}$ 映射到标准化设备坐标(NDC)中的 [-1, 1] 范围。为此,我们需要将 x 坐标从 [-r, r] 映射到 [-1, 1]。
$$ x_{ndc} = \frac{x_{proj}}{r} = \frac{\frac{n}{z} x}{r} = \frac{n x}{r z} $$
由于 r = t*aspectRatio = n * tan(θ) * aspectRatio,我们可以进一步简化:
$$ x_{ndc} = \frac{n x}{n \cdot \tan(\theta) \cdot \text{aspectRatio} \cdot z} = \frac{x}{\tan(\theta) \cdot \text{aspectRatio} \cdot z} $$
注意: 在透视投影矩阵中, 上面得到的这个计算过程是通过透视投影矩阵的乘法和透视除法实现的。同时说明 $x_{ndc}$ 的大小 跟z轴坐标的大小成反比。
# 2. y轴映射
我们需要将 y 坐标从 [−t,t] 映射到 [−1,1]。
类似地,我们考虑在近平面上的投影点 ($x_{proj}$ ,$x_{proj}$,n) 。根据相似三角形原理:
$$
\frac{y_{proj}}{y} = \frac{n}{z} \Rightarrow y_{proj} = \frac{n}{z} y
$$
然后将 $y_{proj}$ 映射到标准化设备坐标(NDC)中的 [-1, 1] 范围。为此,我们需要将 x 坐标从 [-t, t] 映射到 [-1, 1]。
$$
y_{ndc} = \frac{y_{proj}}{t} = \frac{\frac{n}{z} y}{r} = \frac{n y}{t z}
$$
由于 t=n*tan(θ),我们可以进一步简化:
$$
y_{ndc} = \frac{n y}{n \cdot tan(\theta) \cdot z}
= \frac{y}{tan(\theta) \cdot z}
$$
注意: 在透视投影矩阵中, 上面得到的这个计算过程是通过透视投影矩阵的乘法和透视除法实现的。同时说明 $y_{ndc}$ 的大小 跟z轴坐标的大小成反比。
# 3. z轴映射
我们需要将 z 坐标从 [n,f] 映射到 [-1,1]。对于 z 轴映射,我们希望在近平面和远平面之间进行线性变换。
线性变换的标准公式为:
$$
z_{proj} = A \cdot z + B
$$
我们通过透视除法将齐次坐标转换到标准化设备坐标,这里的w分量我们使用-z表示。:
$$
z_{ndc} = \frac{z_{proj}}{w} = \frac{z_{proj}}{-z}
= \frac{A \cdot z + B}{-z}
= -A - \frac{B}{z}
$$
我们希望满足以下条件:
$$ z = n \Rightarrow z_{ndc} = -1 $$ $$ z = f \Rightarrow z_{ndc} = 1 $$
通过代入以上条件,我们可以得到两个方程:
$$ -1 = - A + \frac{B}{n} $$
$$ 1 = - A + \frac{B}{f} $$
解这组方程:
$$ -A + \frac{B}{n} = -1 $$
$$ -A + \frac{B}{f} = 1 $$
相减得到:
$$ \frac{B}{f} - \frac{B}{n} = 2 \Rightarrow B = \frac{2fn}{n - f} $$
代入 $$ -1 = - A + \frac{B}{n}\Rightarrow A = \frac{B}{n} + 1 = \frac{\frac{2fn}{n - f}}{n} + 1 = \frac{2f}{n-f} + 1 = \frac{f+n}{n-f} $$
因此,z 轴的线性变换为:
$$ z_{ndc} = -\frac{f+n}{n-f} - \frac{2fn}{n - f} \cdot \frac{1}{z} $$ 那么经过透视除法之前的裁剪坐标系中的坐标应该是 $$ z_{ndc} \cdot -z = \frac{f+n}{n-f} \cdot + \frac{2fn}{n - f} $$
# 4.透视投影矩阵的构建
将上述公式整合到一个矩阵中,我们得到透视投影矩阵:
$$ \mathbf{P}_{perspective} = \begin{bmatrix} \frac{n}{r} & 0 & 0 & 0 \ 0 & \frac{n}{t} & 0 & 0 \ 0 & 0 & -\frac{f + n}{f - n} & -\frac{2fn}{f - n} \ 0 & 0 & -1 & 0 \end{bmatrix} $$
参考文档
WebGL 三维透视投影 (opens new window)
透视投影 (opens new window)