# 1.正交投影
正交投影的可视空间由前面两个矩形表面确定。分别是近裁剪面和远裁剪面。
canvas上显示的是可视空间中的物体在近裁剪面上的投影。
正交投影看到的物体都是一样大的,跟模型距离观察者的距离没有关系。
正交投影,可视范围是一个长方体盒子。
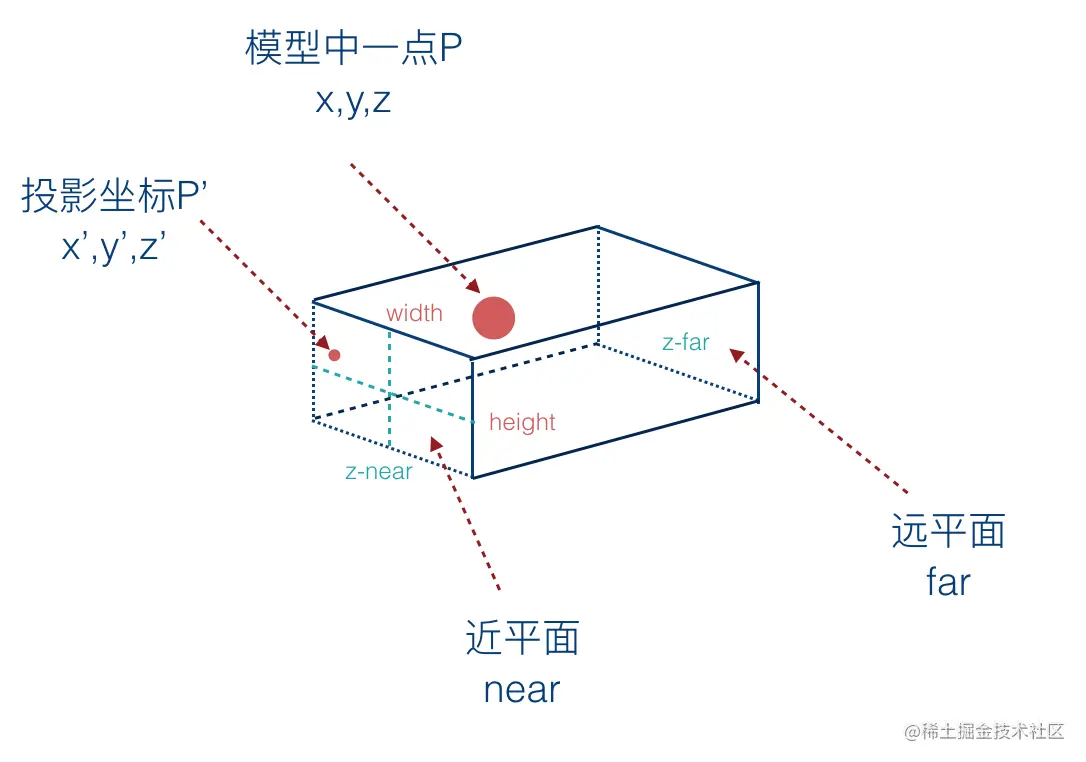
接下来我们将推导一下正交投影的矩阵是如何得到的。
假设模型中有一个点p(x,y,z)表示像素坐标,投影到近平面后的坐标为p'(x',y',z'),表示投影坐标。
那么 p和p'之间的关系是怎样的呢?首先我们的已知条件是.
x坐标在[-width/2, width / 2]之间,通常我们不指定width,而是指定相机坐标系下的投影盒的左右两侧坐标,left和right。y坐标在[-height/2, height/2]之间,通常我们不指定height,而是指定相机坐标系下的投影盒的左右两侧坐标,top和bottom。z坐标在[zNear, zFar]之间。
投影后的点 p'(x',y',z'),其中:
x'在[-1,1]之间y'在[-1,1]之间z'在[-1,1]之间
# 2.正交投影矩阵的推导
首先我们需要找出 p和 p'之间的关系。p和p'之间的关系可以用如下矩阵来表示。
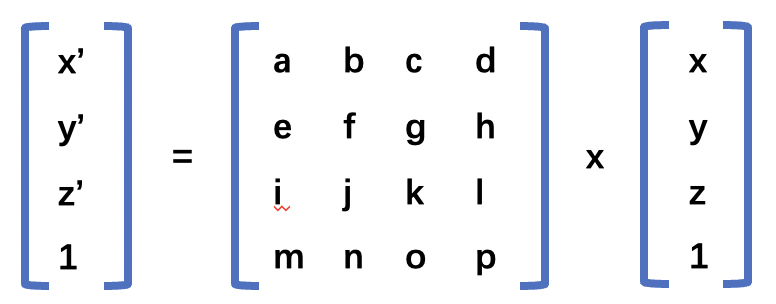
上面的矩阵运算后可以得到下面的计算结果。
x' = ax + by + cz + d
y' = ex + fy + gz + h
z' = ix + jy + kz + l
1 = mx + ny + oz + p
1
2
3
4
2
3
4
# 1. x' 和 x 的关系
我们先将 p 点的 x上的坐标投影到近平面上。首先我们知道有这么一个对应关系。根据长方体来根据近平面来计算得出一个坐标系。在近平面上我们可以得到下面的信息。
(left+right)/2 为 x轴的原点(x轴方向的中心点)
(right-left)/2 为 x的正向最大值,也就是width/2
(left-right)/2 为 x的负向最大值
1
2
3
2
3
那么x' 和 x 的关系可以用如下的计算公式来表示。将屏幕坐标转换成投影坐标
x' = (x- (left+right)/2)/(right-left)/2
= 2(x- (left+right)/2)/(right-left)
= 2x/(right-left) - (left+right)/(right-left)
1
2
3
2
3
上面的公式中
(x- (left+right)/2) 表示 x 相对于坐标原点的距离
(right-left)/2 为 x 的正向最大值,也就是 width/2
1
2
2
# 2. y' 和 y 的关系
我们先将p点的 y上的坐标投影到近平面上。在近平面上我们也可以得到下面的信息
(bottom+top)/2 为 y轴的原点(x轴方向的中心点)
(top-bottom)/2 为 y的正向最大值,也就是height/2
(bottom-top)/2 为 y的负向最大值
1
2
3
2
3
那么y' 和 y 的关系可以用如下的计算公式来表示。
y' = (y- (top+bottom)/2)/(top-bottom)/2
= (2y- (top+bottom))/(top-bottom)
= 2y/(top-bottom) - (top+bottom)/(top-bottom)
1
2
3
2
3
# 3. z' 和 z 的关系
z' = (z- (zFar+zNear)/2)/(zFar-zNear)/2
= (2z- (zFar+zNear))/(zFar-zNear)
= 2z/(zFar-zNear) - (zFar+zNear)/(zFar-zNear)
1
2
3
2
3
上面的公式中
(z- (zFar+zNear)/2) 表示 z 相对于坐标原点的距离
(zFar-zNear)/2 为 z 的正向最大值,也就是 depth/2
1
2
2
根据上面的计算公式,我们计算一下矩阵相乘的结果,可以得到下面的表达式。
x' = ax + by + cz + d = 2x/(right-left) - (left+right)/(right-left)
y' = ex + fy + gz + h = 2y/(top-bottom) - (top+bottom)/(top-bottom)
z' = ix + jy + kz + l = 2z/(zFar-zNear) - (zFar+zNear)/(zFar-zNear)
1 = mx + ny + oz + p = 1
1
2
3
4
2
3
4
根据上面得到的计算结果,即可求出正交投影矩阵。

用 JavaScript 实现正交投影矩阵的代码则如下所示
function orthographic(left, right, bottom, top, near, far) {
return [
2 / (right - left), 0, 0, 0,
0, 2 / (top - bottom), 0, 0,
0, 0, -2 / (far - near), 0,
-(right + left) / (right - left), -(top + bottom) / (top - bottom), -(far + near) / (far - near), 1
];
}
// 示例
const left = -1, right = 1, bottom = -1, top = 1, near = -1, far = 1;
const orthoMatrix = orthographic(left, right, bottom, top, near, far);
console.log("Orthographic Projection Matrix:", orthoMatrix);
1
2
3
4
5
6
7
8
9
10
11
12
13
2
3
4
5
6
7
8
9
10
11
12
13
总结: 计算正交投影的关键是要求出 p 和 p' 之间的关系,及屏幕坐标跟投影坐标的关系。
阅读量: