# 1.顶点的绘制顺序
在默认情况下,WebGL为了加速绘图操作,是按照顶点在缓冲区中的顺序来处理它们的。下面是顶点数据。
const verticesColors = new Float32Array([
// Vertex coordinates and color
0.0, 1.0, -4.0, 0.4, 1.0, 0.4, // The back green one
-0.5, -1.0, -4.0, 0.4, 1.0, 0.4,
0.5, -1.0, -4.0, 1.0, 0.4, 0.4,
0.0, 1.0, -2.0, 1.0, 1.0, 0.4, // The middle yellow one
-0.5, -1.0, -2.0, 1.0, 1.0, 0.4,
0.5, -1.0, -2.0, 1.0, 0.4, 0.4,
0.0, 1.0, 0.0, 0.4, 0.4, 1.0, // The front blue one
-0.5, -1.0, 0.0, 0.4, 0.4, 1.0,
0.5, -1.0, 0.0, 1.0, 0.4, 0.4,
]);
2
3
4
5
6
7
8
9
10
11
12
13
14
按照绘制顺序,绿色的三角形在最下面,紫色的三角形在最上面。如下图所示。
实例 demo 地址 (opens new window)

当我们将顶点数据做如下修改时,改变顶点的深度值(z轴坐标),使绿色三角形>黄色三角形>紫色三角形。
const verticesColors = new Float32Array([
// Vertex coordinates and color
0.0, 1.0, 2.0, 0.4, 1.0, 0.4, // The back green one
-0.5, -1.0, 2.0, 0.4, 1.0, 0.4,
0.5, -1.0, 2.0, 1.0, 0.4, 0.4,
0.0, 1.0, 1.0, 1.0, 1.0, 0.4, // The middle yellow one
-0.5, -1.0, 1.0, 1.0, 1.0, 0.4,
0.5, -1.0, 1.0, 1.0, 0.4, 0.4,
0.0, 1.0, 0.0, 0.4, 0.4, 1.0, // The front blue one
-0.5, -1.0, 0.0, 0.4, 0.4, 1.0,
0.5, -1.0, 0.0, 1.0, 0.4, 0.4,
]);
2
3
4
5
6
7
8
9
10
11
12
13
14
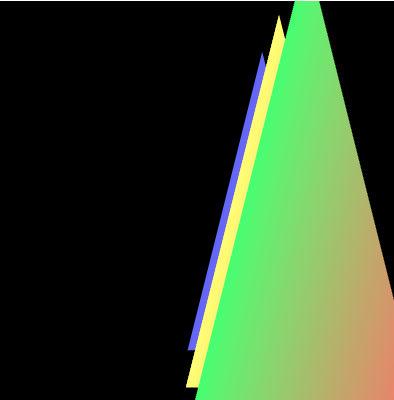
绘制结果如下图所示。紫色的三角形还是在上面

这样看的可能还不太明显,我们可以将三角形进行一定角度的旋转。
modelMatrix.setTranslate(0, 0, 0).setRotate(-10,0,1,0);
我们可以得到下面的渲染效果

可以看到三角形是按照右手坐标系,绕 Y 轴旋转了10度,那也就是按照左手坐标系,绕 Y 轴旋转了-10度,同时也可以看出,绿色的三角形是在最下面的。这也证明了没有开启深度测试之前,是按照顶点在缓冲区中的顺序绘制的。
为了进一步验证顶点的绘制顺序问题,我们再次修改一下顶点的顺序。
const verticesColors = new Float32Array([
0.0, 1.0, 1.0, 1.0, 1.0, 0.4, // yellow one
-0.5, -1.0, 1.0, 1.0, 1.0, 0.4,
0.5, -1.0, 1.0, 1.0, 0.4, 0.4,
// Vertex coordinates and color
0.0, 1.0, 2.0, 0.4, 1.0, 0.4, // green one
-0.5, -1.0, 2.0, 0.4, 1.0, 0.4,
0.5, -1.0, 2.0, 1.0, 0.4, 0.4,
0.0, 1.0, 0.0, 0.4, 0.4, 1.0, // blue one
-0.5, -1.0, 0.0, 0.4, 0.4, 1.0,
0.5, -1.0, 0.0, 1.0, 0.4, 0.4,
]);
2
3
4
5
6
7
8
9
10
11
12
13
为了使效果看起来更明显,我们将三角形进行一定角度的旋转。
// 绕y轴旋转
modelMatrix.setTranslate(0, 0, 0).setRotate(-10,0,1,0);
2
我们可以得到下面的渲染效果,紫色的三角形在最上面。

# 2.开启深度测试
为了让WebGL按照z 轴坐标值的大小来绘制,WebGL提供了 开启深度测试 的功能。这个功能的作用就是将那些被遮挡的面清除掉。开启隐藏面清除功能,需要遵循以下3个步骤。
1.开启深度测试
gl.enable(gl.DEPTH_TEST)。//开启深度测试
2.在绘制之前,清除深度缓冲区。
gl.clear(gl.DEPTH_BUFFER_BIT);
WebGL在颜色缓冲区中绘制几何图形,绘制完成后将颜色缓冲区显示到canvas上。而深度缓冲区就是用来存储深度信息的。由于深度方向通常是Z轴方向,所以有时候我们也称之为Z轴缓冲区。
3.正确设置可视空间,也就是进行投影变换
进行投影变换实际上是为了将坐标系转变称我们熟悉的右手坐标系,也就是z轴正向朝向屏幕外。
经过上面的三部曲操作后,绘制结果如下图所示:
此时 z 值最大的绿色三角形在最上面,其次使黄色三角形,最底下的而是紫色三角形。
gl.enable()函数是用来开启WebGL中的多种功能的。一般有以下几个参数。
gl.DEPTH_TEST:隐藏面清除
gl.BLEND: 混合
gl.POLYGON_OFFSET_FILL: 多边形位移
2
3
# 3.深度冲突
当几何图形的两个表面极为接近时,会出现问题,表面上看起来斑斑驳驳的,这种现象称之为深度冲突。下面我们来绘制两个Z值完全一致的三角形来进行测试。
顶点数据如下所示:
var verticesColors = new Float32Array([
// Vertex coordinates and color
0.0, 2.5, -5.0, 0.4,1.0,0.4, // The green triangle
-2.5,-2.5,-5.0, 0.4,1.0,0.4,
2.5, -2.5,-5.0, 1.0,0.4,0.4,
0.0, 3.0, -5.0, 1.0,0.4,0.4, // The yellow triagle
-3.0,-3.0,-5.0, 1.0,1.0,0.4,
3.0, -3.0,-5.0, 1.0,1.0,0.4
])
2
3
4
5
6
7
8
9
10
demo地址 (opens new window)
绘制结果如下所示:

WebGL为了解决这个问题,提供了一种多边形偏移的机制来解决这个问题。该机制将自动在z值上添加一个偏移量,偏移量的值由物体表面相对于观察者视线的角度来确定。启动该机制只需要两行代码。
- 启用多边形偏移。
gl.enable(gl.POLYGON_OFFSET_FILL)
- 在绘制之前指定用来计算偏移量的参数。
gl.polygonOffset(1.0, 1.0)
gl.polygonOffset(factor, units)偏移量按照公式m*factor+r*units计算,其中m表示顶点所在表面相对于观察者的视角的角度,而r表示硬件能够区分两个z值之差的最小值。
开启多边形偏移后的绘制结果如下所示。
# 4.投影矩阵对顶点绘制的影响
# 4.1 不使用投影矩阵
下面是不开启深度测试的情况
- 顶点着色器中的代码
attribute vec4 a_Position;
attribute vec4 a_Color;
varying vec4 v_Color;
void main() {
gl_Position = a_Position;
v_Color = a_Color;
}
2
3
4
5
6
7
js中的顶点坐标代码
const pc = new Float32Array([ // Vertex coordinates and color
0.0, 0.5, 0.1, 0.0, 0.0, 1.0, // The front blue one
-0.5, -0.5, 0.1, 0.0, 0.0, 1.0,
0.5, -0.5, 0.1, 1.0, 1.0, 0.0,
0.5, 0.4, -0.5, 1.0, 1.0, 0.0, // The red triangle is behind
-0.5, 0.4, -0.5, 1.0, 0.0, 0.0,
0.0, -0.6, -0.5, 1.0, 0.0, 0.0,
]);
2
3
4
5
6
7
8
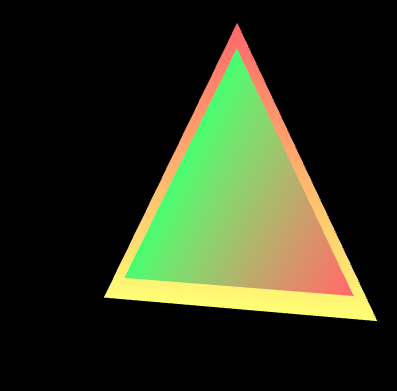
9
分析:从上面的顶点坐标以及颜色的代码,我们可以知道 z轴坐标为 -0.1的三角形的顶点颜色蓝色和黄色。z轴坐标为 -0.5的三角形的顶点颜色红色和黄色。
按照右手坐标系,理论上, z轴坐标为 -0.1的三角形应该在 z轴坐标为 -0.5的上面。然后实际的结果如下图所示, z轴坐标为 -0.5的三角形在上面。
视觉效果如下图所示:

当我们改变顶点坐标的绘制顺序时。
const pc = new Float32Array([ // Vertex coordinates and color
0.5, 0.4, -0.5, 1.0, 1.0, 0.0, // The red triangle is behind
-0.5, 0.4, -0.5, 1.0, 0.0, 0.0,
0.0, -0.6, -0.5, 1.0, 0.0, 0.0,
0.0, 0.5, 0.1, 0.0, 0.0, 1.0, // The front blue one
-0.5, -0.5, 0.1, 0.0, 0.0, 1.0,
0.5, -0.5, 0.1, 1.0, 1.0, 0.0,
]);
2
3
4
5
6
7
8
视觉效果如下所示

下面是不使用投影矩阵绘制顶点的两个demo。
z值小的顶点后绘制 (opens new window) z值小的顶点先绘制 (opens new window)
开启深度测试的情况
开启深度测试后,不管顶点坐标的绘制顺序是怎样的,顶点的颜色由顶点的深度(z值)所决定,同一位置的顶点,其颜色由z值最靠近视点的顶点决定(这里的z值,说的时NDC坐标系中(左手坐标系,z轴指向屏幕里面)的坐标)。
const pc = new Float32Array([ // Vertex coordinates and color
0.5, 0.4, -0.5, 1.0, 1.0, 0.0, // The red triangle is behind
-0.5, 0.4, -0.5, 1.0, 0.0, 0.0,
0.0, -0.6, -0.5, 1.0, 0.0, 0.0,
0.0, 0.5, 0.1, 0.0, 0.0, 1.0, // The front blue one
-0.5, -0.5, 0.1, 0.0, 0.0, 1.0,
0.5, -0.5, 0.1, 1.0, 1.0, 0.0,
]);
//或者
const pc2 = new Float32Array([ // Vertex coordinates and color
0.0, 0.5, 0.1, 0.0, 0.0, 1.0, // The front blue one
-0.5, -0.5, 0.1, 0.0, 0.0, 1.0,
0.5, -0.5, 0.1, 1.0, 1.0, 0.0,
0.5, 0.4, -0.5, 1.0, 1.0, 0.0, // The red triangle is behind
-0.5, 0.4, -0.5, 1.0, 0.0, 0.0,
0.0, -0.6, -0.5, 1.0, 0.0, 0.0,
]);
...
gl.enable(gl.DEPTH_TEST);
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
上面开启深度测试的顶点绘制的图形如下所示

const pc = new Float32Array([ // Vertex coordinates and color
0.0, 0.5, 0.1, 0.0, 0.0, 1.0, // The front blue one
-0.5, -0.5, 0.1, 0.0, 0.0, 1.0,
0.5, -0.5, 0.1, 1.0, 1.0, 0.0,
0.5, 0.4, 0.5, 1.0, 1.0, 0.0, // The red triangle is behind
-0.5, 0.4, 0.5, 1.0, 0.0, 0.0,
0.0, -0.6, 0.5, 1.0, 0.0, 0.0,
]);
//或者
const pc2 = new Float32Array([ // Vertex coordinates and color
0.5, 0.4, 0.5, 1.0, 1.0, 0.0, // The red triangle is behind
-0.5, 0.4, 0.5, 1.0, 0.0, 0.0,
0.0, -0.6, 0.5, 1.0, 0.0, 0.0,
0.0, 0.5, 0.1, 0.0, 0.0, 1.0, // The front blue one
-0.5, -0.5, 0.1, 0.0, 0.0, 1.0,
0.5, -0.5, 0.1, 1.0, 1.0, 0.0,
]);
...
gl.enable(gl.DEPTH_TEST);
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
上面开启深度测试的顶点绘制的图形如下所示

# 5.2 使用投影矩阵
但我们使用投影矩阵后,通过设置正射投影矩阵中的远、近平面的位置,我们看到的结果又会不一样。
注意: 使用投影矩阵时,都会默认开启深度测试,开启深度测试后的顶点的颜色由顶点的深度(z值)所决定,同一位置的顶点,其颜色由z值最大的顶点决定(这里的z值,说的时NDC坐标系中的坐标)。
gl.enable(gl.DEPTH_TEST);
- 顶点着色器中的代码
attribute vec4 a_Position;
attribute vec4 a_Color;
uniform mat4 u_MvpMatrix;
varying vec4 v_Color;
void main() {
gl_Position = u_MvpMatrix * a_Position;
v_Color = a_Color;
}
2
3
4
5
6
7
8
js中的顶点坐标代码
const pc = new Float32Array([ // Vertex coordinates and color
0.0, 0.5, -0.1, 0.0, 0.0, 1.0, // The front blue one
-0.5, -0.5, -0.1, 0.0, 0.0, 1.0,
0.5, -0.5, -0.1, 1.0, 1.0, 0.0,
0.5, 0.4, -0.5, 1.0, 1.0, 0.0, // The red triangle is behind
-0.5, 0.4, -0.5, 1.0, 0.0, 0.0,
0.0, -0.6, -0.5, 1.0, 0.0, 0.0,
]);
2
3
4
5
6
7
8
9
- 设置投影矩阵。
const u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
const mvpMatrix = new Matrix4();
// setOrtho(left,right,bottom,top,near,far)
mvpMatrix.setOrtho(-1, 1, -1, 1, 1, -1); // Set the viewing volume
// Pass the view matrix to u_MvpMatrix
gl.uniformMatrix4fv(u_MvpMatrix, false, mvpMatrix.elements);
2
3
4
5
6
7
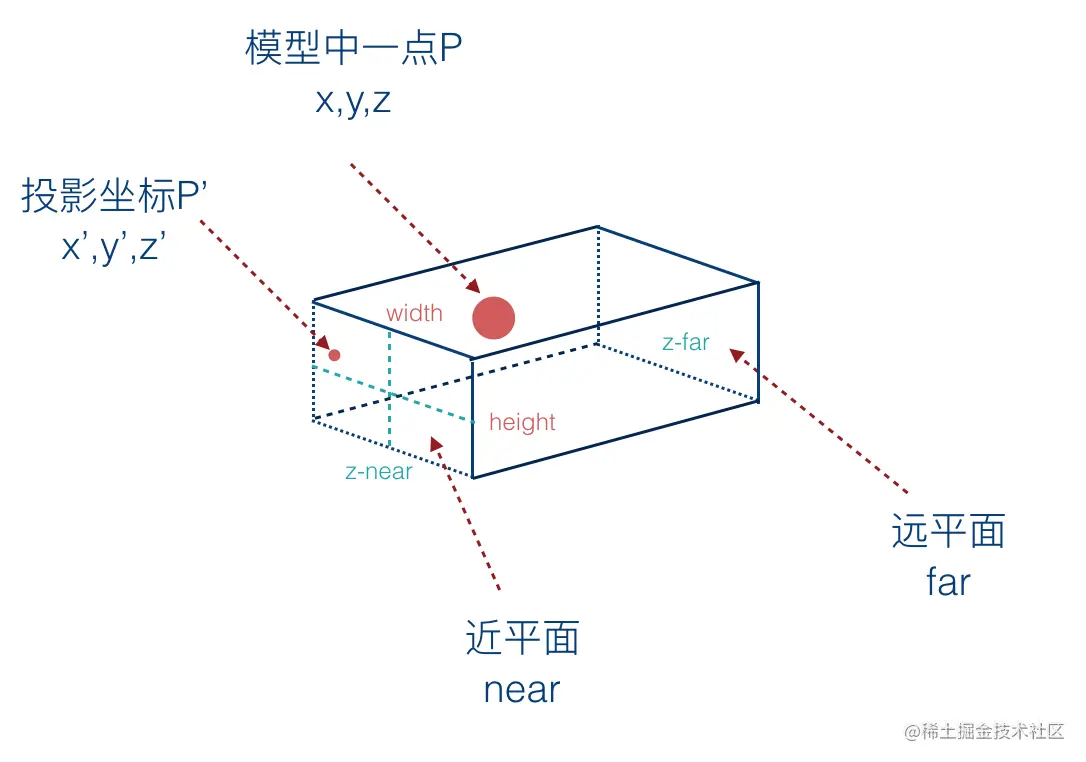
根据正射矩阵的公式,如下图所示。
下面我们又看下通过设置远、近平面的大小关系来观察看到的实际效果。
near>far的正交投影
我们将 left=-1,right=1,bottom=-1,top=1,near=1,far= -1 代入上面的矩阵可以得到如下的单位矩阵。
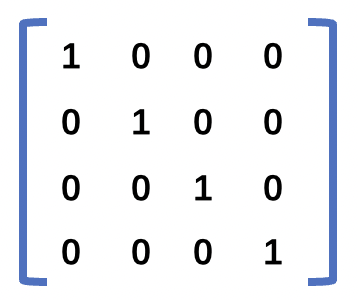
根据正射投影的示意图。再结合 near = 1 要比far =-1大,表示在视线方向上,远裁剪面(或者叫远平面)实际在近裁剪面(或者叫近平面) 的前面,表示我们将远近截面 做了旋转180度,将z轴正向朝向屏幕里面,这是刚好跟左手坐标系一样。
通过上面的参数设置的正交投影矩阵, 可以得出结论:当正射矩阵中的near>far时,WebGL就会使用左手坐标系统。此时看到的效果还是会跟之前一样。就算我们改变顶点的绘制顺序,最终的视觉效果都是一样的,都如下图所示

demo地址为 使用投影矩阵(near>far) (opens new window)。
near<far的正交投影
但是如果我们将参数做以下调整。
mvpMatrix.setOrtho(-1, 1, -1, 1, -1, 1);
我们将 left=-1,right=1,bottom=-1,top=1,near=-1,far= 1 代入上面的矩阵可以得到如下的矩阵。
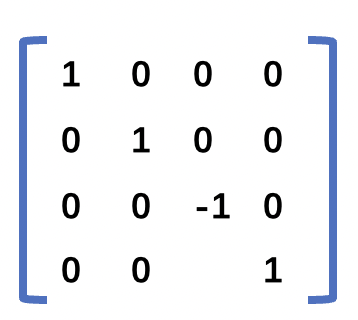
而且不管我们是否改变顶点的绘制顺序,都可以得到如下效果图。

现在我们看到的才是 z=-0.1三角形在 z=-0.5的三角形的上面。根据上面的矩阵,我们可以看到我们实际上是将坐标沿z轴,做了-1的缩放。此时我们可以将坐标系看成是z轴正向朝屏幕外的坐标系,也就是我们常说的右手坐标系。
demo地址为使用投影矩阵(near<far) (opens new window)
结论: 使用正交投影后的坐标,然后根据深度测试,以及左手坐标系,同一个位置的颜色由z值最小的顶点决定。
